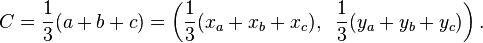Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

"The centroid of a triangle divides each of the median in the ratio 2:1.." Can u plsss explain this sentence with the help of a diagram..??
Asked by Sneha George | 25 Feb, 2011, 03:17: AM
answered-by-expert Expert Answer

Dear Student,

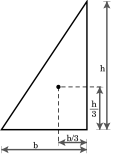
The centroid of a triangle is the point of intersection of its medians (the lines joining each vertex with the midpoint of the opposite side). The centroid divides each of the medians in the  ratio 2:1, which is to say it is located ⅓ of the perpendicular distance between each side and the opposing point (see figures). Its Cartesian coordinates are the means of the coordinates of the three vertices. That is, if the three vertices are a = (xa,ya), b = (xb,yb), and c = (xc,yc), then the centroid is

 

 

The centroid is therefore at \left(\frac13,\frac13,\frac13\right) in barycentric coordinates.

    
 
Regards
Team Topperlearning.
Answered by | 25 Feb, 2011, 09:29: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
The distance of the point (5,-2) from x-axis will be :-
Asked by pathakvaishnavi9139 | 23 Mar, 2024, 10:45: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
a
Asked by Chavvatejdeepreddy | 27 Feb, 2024, 06:43: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
find the point on the y-axis which equidistant from (4,1)and (-3,5)
Asked by jdharmendra097 | 21 Feb, 2024, 08:02: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
the foot of the perpendicular from P(-3,2) to y-axis I M. coordinates of M are....
Asked by raj.mehta2006 | 21 Feb, 2024, 11:23: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
find the points which divide the line segments joining the points (1 , 7 ) (- 6 , - 3) in the ratio of 2:3
Asked by lakshmidasari280 | 29 Jan, 2024, 07:44: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
assumes that is unit is 1 km to answer the following question the coordinates given below are given from a base station xyz airport find the distance between two aeroplan in kilometre which are at location A and B If a line on the y- axis and has an ordinate 1.5 will B lines on the x axis and has and abscissa 0.5 ..
Asked by namansinghnamansinghdelhi | 22 Dec, 2023, 10:44: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
2+2
Asked by kabitamula124 | 20 Dec, 2023, 11:59: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
What is locus
Asked by kavitayadav9001419917 | 23 Nov, 2023, 08:14: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
at what point the origin be shifted so that the point 3 2 are seen the position at -34
Asked by sufibadole08 | 19 Nov, 2023, 09:13: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
find the centroid of the triangles with vertices: (-1,3),(6,-3) and (-3,6)
Asked by kadaramyadav | 02 Nov, 2023, 11:02: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×