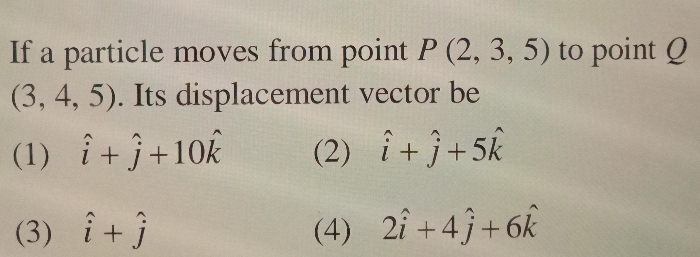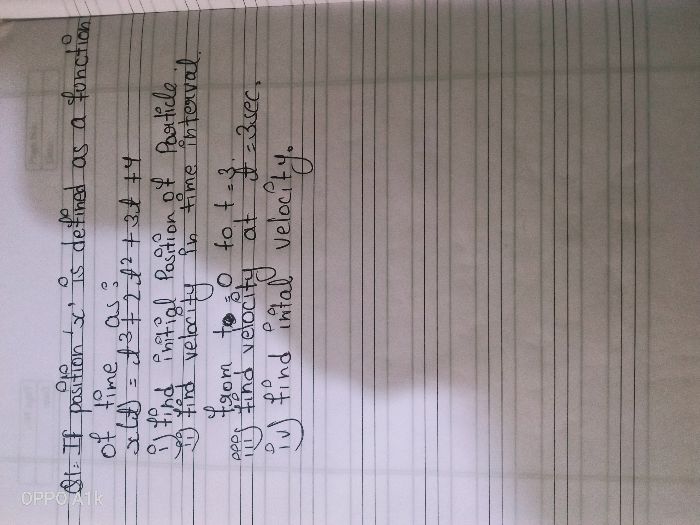CBSE Class 11-science Answered
The 2 ends of train ,moving with a constant acceleration,pass a certain with velocity u and v .Show that velocity with which the middle point of train passes the same point is root of(usquare +v square)/2
Asked by ajaysekharjs | 27 Aug, 2018, 11:54: AM
Using the equation of kinematics for velocities, acceleration and displacement,

At the velocity at the mid-point of the train is vm
and that can be found using the same kinematical equation.
At the midpoint, the 'u' is zero and the displacement made is,
sm , such that sm = s/2.

Using equation (a) and (b)

Hence it is proved that the velocity of a train at its midpoint is the square root of half of the difference of the squares of their final and initial velocity.
Answered by Abhijeet Mishra | 28 Aug, 2018, 02:28: PM
Concept Videos
CBSE 11-science - Physics
Asked by manjusrihalder395 | 07 Jan, 2024, 09:55: PM
CBSE 11-science - Physics
Asked by spandya632 | 17 Nov, 2023, 08:36: AM
CBSE 11-science - Physics
Asked by hy9022075 | 10 Jan, 2023, 09:06: PM
CBSE 11-science - Physics
Asked by ad4957216 | 03 Jan, 2023, 04:54: PM
CBSE 11-science - Physics
Asked by prashantgaikwadfox000 | 25 Sep, 2022, 05:38: PM
CBSE 11-science - Physics
Asked by ukalyadab | 18 Jul, 2022, 11:52: AM
CBSE 11-science - Physics
Asked by piyushhoney2006 | 20 Jun, 2022, 04:12: PM
CBSE 11-science - Physics
Asked by chinttubabu9692 | 27 Jan, 2022, 06:37: PM