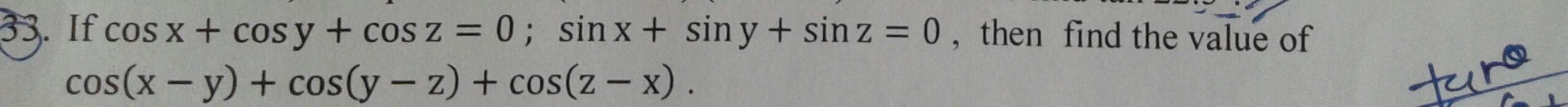CBSE Class 11-science Answered
tan x =n tan y n belongs to R+ then maximum value of sec^2(x-y)=(n+1)^2/4n
Asked by aahnik.mohanty | 29 May, 2019, 08:04: PM
cos (x - y) = cosx cosy + sinx siny
= cosx cosy (1 + tanx tany)
= cosx cosy (1 + ntan2 y)
sec2 (x - y) = 1/cos2 (x - y)
= sec2 x sec2 y/(1 + ntan2 y)2
= (1 + tan2 x)(1 + tan2 y)/ (1 + ntan2 y)2
= (1 + ntan2 y)(1 + tan2 y)/(1 + ntan2 y)2
Solving we get
sec2 (x - y) = [1 + (n - 1)2 tan2 y]/(1 + ntan2 y)2
1 + ntan2 y ≥ ntan2 y
[(1 + ntan2 y)/2]2 ≥ ntan2 y AM ≥ GM
tan2 y/(1 + ntan2 y)2 ≤ 1/4n
sec2 (x - y) ≤ 1 + (n - 1)2/4n = (n + 1)2/4n
Answered by Sneha shidid | 30 May, 2019, 10:13: AM
Concept Videos
CBSE 11-science - Maths
Asked by rajyothi64 | 05 Mar, 2024, 09:49: PM
CBSE 11-science - Maths
Asked by surekhashriwas01 | 12 Sep, 2023, 08:39: PM
CBSE 11-science - Maths
Asked by vinay123chintu | 08 Jun, 2023, 08:41: PM
CBSE 11-science - Maths
Asked by soumyadas098h | 02 Nov, 2022, 08:01: PM
CBSE 11-science - Maths
Asked by vermahiteshi243 | 30 Aug, 2021, 09:53: AM
CBSE 11-science - Maths
Asked by bandlapravalika4 | 25 Sep, 2020, 01:32: PM
CBSE 11-science - Maths
Asked by Lalit Kariya | 12 Mar, 2020, 03:07: PM
CBSE 11-science - Maths
Asked by aahnik.mohanty | 29 May, 2019, 08:04: PM