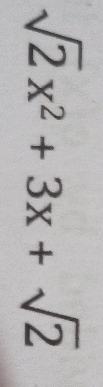CBSE Class 9 Answered
suppose f(x) is a polynomial of degree 5 and with leading coefficient 2009. suppose further that f(1)=1,f(2)=3, f(3)=5,f(4)=7, f(5)=9. what is the value of f(6)
Asked by manvendra singh | 19 Nov, 2013, 10:42: PM
Expert Answer
Let f(x) = g(x) + 2x - 1. Since f(1)=1, f(2)=3, f(3)=5, f(4)=7, f(5)=9, it then follows that g(1) = g(2) = g(3) = g(4) = g(5) = 0.
Since f(x) is 5th degree with leading coefficient 2009, the same is true for g(x).
Therefore, g(x) = 2009(x - 1)(x - 2)(x - 3)(x - 4)(x - 5).
So now, we have
f(x) = 2009(x - 1)(x - 2)(x - 3)(x - 4)(x - 5) + 2x - 1
f(6) = 2009(5)(4)(3)(2)(1) + 12 - 1 = 241091
Answered by | 19 Nov, 2013, 11:32: PM
Application Videos
-
Algebraic Identities: Quadratic
This video contains a question which is solved using square of binomials -
Factorisation using Square identity
This video explains factorisation using square identity -
Factor Theorem 1
This video contains a question which is solved using Factor theorem -
Factor Theorem 2
This video explain an application based problem on Factor theorem. -
Remainder Theorem
This video contains a question which is solved using Remainder theorem
Concept Videos
-
Introduction to Polynomials
This video explains the definition of polynomial and related terms, identif... -
Remainder Theorem
Discuss various algebraic operations on Polynomials. Learn the statement a... -
Factorisation: Factor Theorem
This video explains the factorization of polynomials using Factor Theorem a... -
Algebraic Identities: Quadratic
Understand the Algebraic identities for quadratic Polynomials. Apply the i... -
Algebraic Identities: Cubic Type
Listing of algebraic identities for cubic Polynomials and simplify the comp...
CBSE 9 - Maths
Asked by durgavenkatlakshmi1 | 20 Mar, 2024, 03:56: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by ammudeep0123 | 20 Mar, 2024, 07:13: AM
ANSWERED BY EXPERT
CBSE 9 - Maths
Asked by jaswanthsompi12345 | 19 Dec, 2023, 06:54: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by rizwanmunna406 | 12 Dec, 2023, 10:09: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by sathishdoddamudigere2 | 01 Nov, 2023, 06:53: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by shambhushanker123 | 29 Oct, 2023, 08:36: PM
ANSWERED BY EXPERT
