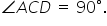CBSE Class 10 Answered
Square ABCD has side length 13,and points E and F are exterior to the square such that BE=DF=5 and AE=CF=12, find EFsquare.
Asked by Kp | 09 Apr, 2017, 07:30: PM
The image is as below:
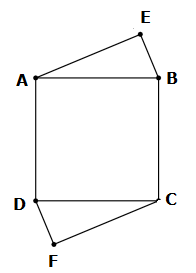
Construction:
Extend AE, DF and BE, CF.
Given square ABCD can be inscribed inside another square EHFG.
Now, length of side of square EHFG = 17 cm.

Answered by Rashmi Khot | 10 Apr, 2017, 09:54: AM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by deepak13376 | 23 Sep, 2020, 01:33: PM
CBSE 10 - Maths
Asked by rhtwatts | 06 Mar, 2019, 03:59: PM
CBSE 10 - Maths
Asked by Topperlearning User | 26 Jul, 2017, 01:58: PM
CBSE 10 - Maths
Asked by Topperlearning User | 26 Jul, 2017, 01:58: PM
CBSE 10 - Maths
Asked by Topperlearning User | 26 Jul, 2017, 01:58: PM
CBSE 10 - Maths
Asked by Topperlearning User | 26 Jul, 2017, 01:58: PM
CBSE 10 - Maths
Asked by Topperlearning User | 26 Jul, 2017, 01:58: PM
CBSE 10 - Maths
Asked by Topperlearning User | 05 Dec, 2013, 08:56: AM
CBSE 10 - Maths
Asked by Topperlearning User | 26 Jul, 2017, 01:58: PM




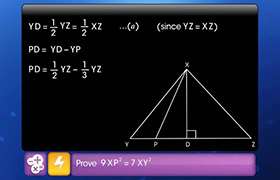

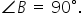 If AD2 = AB2 + BC2 + CD2. Prove that
If AD2 = AB2 + BC2 + CD2. Prove that