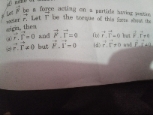CBSE Class 11-science Answered
Solve the following question:
Asked by nkrbasak | 13 Mar, 2012, 09:18: PM
Thin rod of mass m and length ?, rotating around the axis which passes through its center and is perpendicular to the rod.
Let Oz be the axis of rotation, and Ox the axis along the rod. If ? is the density, and s the cross-section of the rod (so that m = ??s), then the volume element for the integral formula will be equal to dV = s·dx, where x changes from ?½? to ½?. The moment of inertia can be found by computing the integral:

- for finding mom of inertia about the axis which is at the one end of the rod and perpendicular to the plane of rod, we have to apply parallel axis theorem.
- so I about the req axis=(1/12 )ml2 +ml2/4
- =ml2 /3
Answered by | 14 Mar, 2012, 10:17: AM
Concept Videos
CBSE 11-science - Physics
Asked by rustampathan | 25 Feb, 2024, 06:39: PM
CBSE 11-science - Physics
Asked by gipaalsy | 08 Feb, 2024, 05:41: AM
CBSE 11-science - Physics
Asked by priyankaprajapti81 | 04 Nov, 2023, 10:47: PM
CBSE 11-science - Physics
Asked by gdeadshot85 | 14 Jan, 2023, 09:58: PM
CBSE 11-science - Physics
Asked by devanshchauhan325 | 23 Dec, 2022, 07:34: AM
CBSE 11-science - Physics
Asked by koushtubhroy | 20 Dec, 2022, 07:36: AM
CBSE 11-science - Physics
Asked by pushpakumari291279 | 20 Aug, 2022, 08:15: AM
CBSE 11-science - Physics
Asked by adipadmakarri | 26 Sep, 2021, 06:08: PM
CBSE 11-science - Physics
Asked by adipadmakarri | 25 Sep, 2021, 11:18: AM