CBSE Class 10 Answered
solution.for this
Asked by ghastipratiksha | 09 Jul, 2020, 06:38: PM
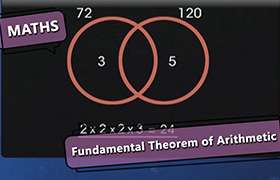
If the number 6n where n belongs to N, were to end with a zero, then its prime factorisation must have 2 and 5 as its factors.
But 6=2 x 3
6n = (2 x 3)n = 2n x 3n
So Prime factors of 6n includes only 2 but not 5.
Also, from the Fundamental theorem of Arithmetic, the prime factorisation of a number is unique.
Hence, a number of the form 6n where n belongs to N, will never end with a zero.
Answered by Yasmeen Khan | 09 Jul, 2020, 08:57: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by bhaskrraobhaskrrao | 18 Jan, 2024, 08:35: PM
CBSE 10 - Maths
Asked by dramu8989 | 02 Dec, 2023, 09:15: PM
CBSE 10 - Maths
Asked by poornimam227 | 30 Nov, 2023, 05:24: PM
CBSE 10 - Maths
Asked by priyanshuaryan895 | 08 Nov, 2023, 07:18: AM
CBSE 10 - Maths
Asked by ruchipandey20071978 | 07 May, 2023, 01:23: PM
CBSE 10 - Maths
Asked by susrisangita792 | 22 Apr, 2023, 09:13: PM
CBSE 10 - Maths
Asked by susrisangita792 | 22 Apr, 2023, 08:52: PM
CBSE 10 - Maths
Asked by susrisangita792 | 20 Apr, 2023, 08:05: AM
CBSE 10 - Maths
Asked by susrisangita792 | 19 Apr, 2023, 08:27: AM










 can end with the digit 0 for any natural number n.
can end with the digit 0 for any natural number n.
