Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

JEE Class main Answered

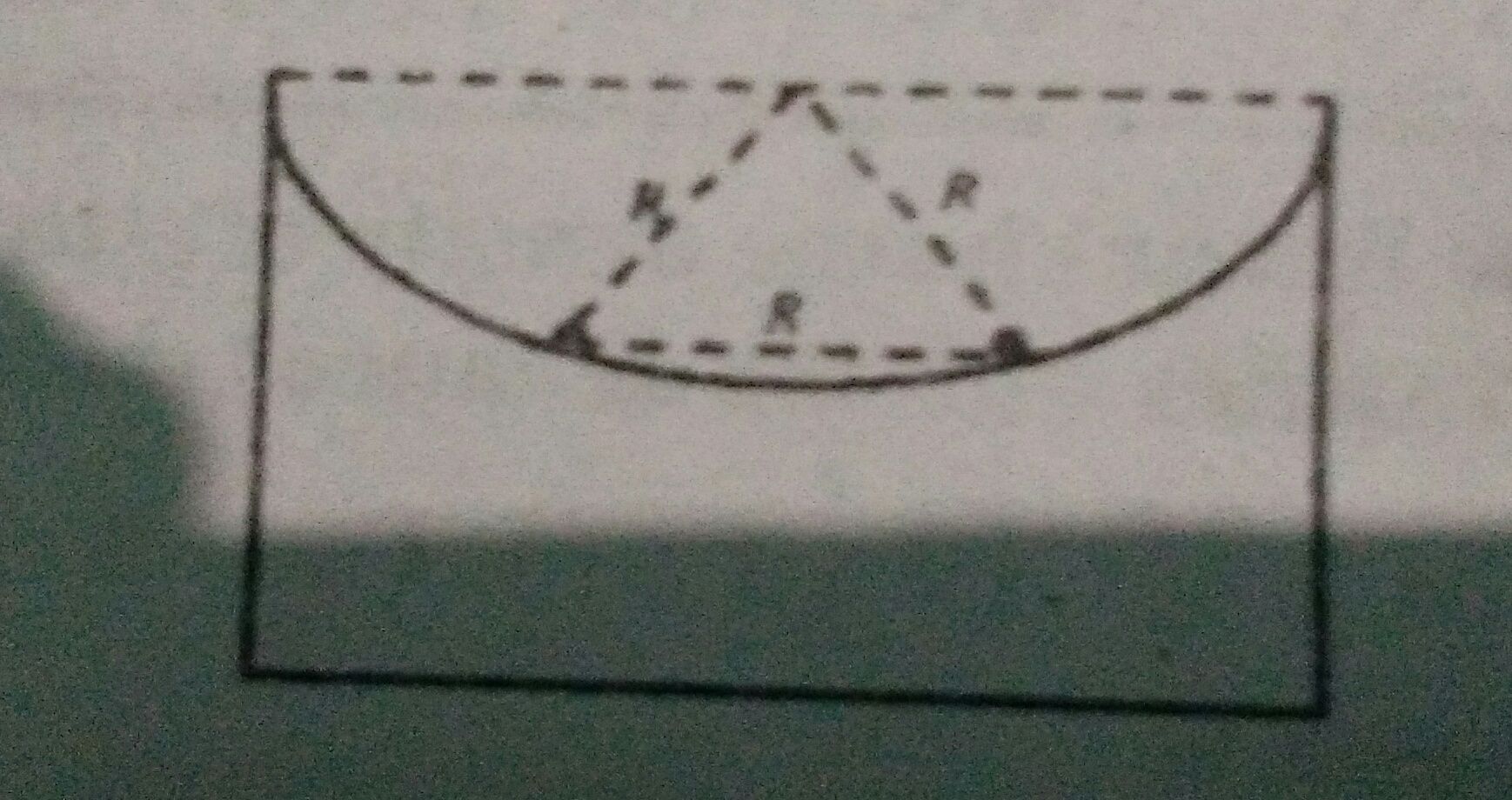
Sir,The gravitational due to a uniform disc at a point in its axis is 2GMr/R²((1/r)-(1/√(r²+R²))).Andthe potential at a point in the axis is -2GM/R²(√(R²+r²)-r) where R-radius and r-distance in the axis. Also,We know that on differentiating gravitational potential we get the gravitational field at that point.But that is not the case for disc.On integrating the potential we are not getting the value of the field.Why is it so? Please help
Asked by das.atom1966 | 16 May, 2022, 05:34: PM
answered-by-expert Expert Answer
Your expression for gravitational force per unit mass due uniform disc is given as
 
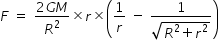begin mathsize 14px style F space equals space fraction numerator 2 G M over denominator R squared end fraction cross times r cross times open parentheses 1 over r space minus space fraction numerator 1 over denominator square root of R squared plus r squared end root end fraction close parentheses end style  .................................(1)
 
where G is universal gravitational constant, M is mass of disc , R is radius of disk and
r is ditance from centre of disc to the point where we are finding gravitational force
 
Above expression is simplified as
 
begin mathsize 14px style F space equals space fraction numerator 2 G M over denominator R squared end fraction cross times open parentheses 1 space minus space fraction numerator r over denominator square root of R squared plus r squared end root end fraction close parentheses end style ..................................(2)
 
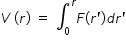
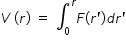
Potential at poit r ,  begin mathsize 14px style V space left parenthesis r right parenthesis space equals space integral subscript 0 superscript r F left parenthesis r apostrophe right parenthesis d r apostrophe end style
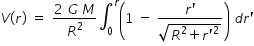
begin mathsize 14px style V left parenthesis r right parenthesis space equals space fraction numerator 2 space G space M over denominator R squared end fraction integral subscript 0 superscript r open parentheses 1 space minus space fraction numerator r apostrophe over denominator square root of R squared plus r apostrophe squared end root end fraction close parentheses space d r apostrophe end style
 
By above integration we get
 
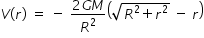begin mathsize 14px style V left parenthesis r right parenthesis space equals space minus space fraction numerator 2 G M over denominator R squared end fraction open parentheses square root of R squared plus r squared end root space minus space r close parentheses end style ..................................(3)
If you want to get Force F(r) from potential , then F(r) = -dV/dr
 
Hence we get gravitational force by differentiating eqn.(3)
 
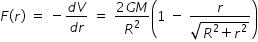
begin mathsize 14px style F left parenthesis r right parenthesis space equals space minus fraction numerator d V over denominator d r end fraction space equals space fraction numerator 2 G M over denominator R squared end fraction open parentheses 1 space minus space fraction numerator r over denominator square root of R squared plus r squared end root end fraction close parentheses end style
Answered by Thiyagarajan K | 16 May, 2022, 09:34: PM
Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
JEE main - Physics
question
question image
Asked by anushkaracha | 14 Mar, 2024, 10:38: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Two identical metal spheres each of diameter 'd ' are kept in contact,then gravitational force is proportional to
Asked by krajasekharnaidu13 | 04 Feb, 2024, 03:37: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
t
question image
Asked by jpmeena2222 | 31 Dec, 2023, 10:27: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Four particles of equal masses are moving round a circle of radius r due to their mutual gravitation attraction. Find the angular velocity.
Asked by aadityakumar0603 | 05 Mar, 2023, 10:17: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
i just want to know why a ball falls on earth when left from a height becuse the gravitional forces of both of them is equal and opposite hence the ball must tend to be at rest in the air .I have already consulted few lecturers but their answer were complicated and tough to understand so i want to get a simpler answer so that i acn understand it in a proper way   
Asked by geethamehs08 | 15 Oct, 2022, 05:54: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
.
question image
Asked by swayamagarwal2114 | 18 Aug, 2022, 09:04: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
plz solve
question image
Asked by swayamagarwal2114 | 21 Jul, 2022, 05:18: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Sir,The gravitational due to a uniform disc at a point in its axis is 2GMr/R²((1/r)-(1/√(r²+R²))).Andthe potential at a point in the axis is -2GM/R²(√(R²+r²)-r) where R-radius and r-distance in the axis. Also,We know that on differentiating gravitational potential we get the gravitational field at that point.But that is not the case for disc.On integrating the potential we are not getting the value of the field.Why is it so? Please help
Asked by das.atom1966 | 16 May, 2022, 05:34: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
gravitation  
Asked by bathularohith19 | 27 Mar, 2022, 03:05: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Two identical beeds each have a mass 'm' and charge 'q' when placed in a hemi spherical bowl of radius 'R' with frictionless and non-conducting walls, the beads move and at equilibrium they are at a separation 'R' as shown in figure. The charge on each bead is
question image
Asked by anshuman.anshuman090 | 07 Apr, 2019, 09:26: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×