CBSE Class 12-science Answered
Sir/Maa'm,
Its my request to solve this tommorow itself its very urgent
as my test approaches so early
i need answer in picture form so i could take printout
question attached below
regards,

Asked by rahmanafeef | 28 Mar, 2020, 10:50: PM
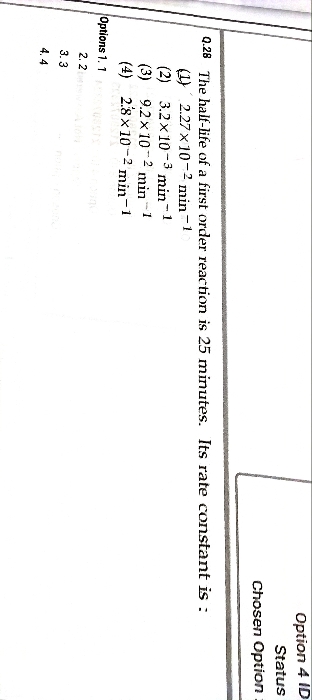
Qn.(1)
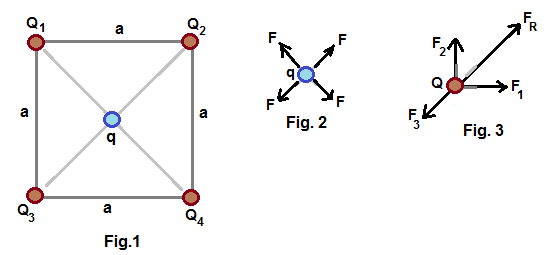
Forces on central charge are getting balanced as shown in fig.2 , because equal forces acting on opposite direction.
Forces acting on the charges placed at corner are shown in fig.3. F1 and F2 are the forces acting through sides of square.
FR is the resultant of F1 , F2 and the force of repulsion due to charge Q placed at the corner along diagonal of square.
F3 is the force acting through diagonal due to charge q at centre. Hence FR balances F3 to get equilibrium .
If charges Q are positive then charge q has to be -ve to balance FR and F3.
Resultant of F1 and F2 = √2 × { Q2 / ( 4πεo a2 ) }
FR = { √2 × [ Q2 / ( 4πεo a2 ) ] } + { [ Q2 / ( 4πεo 2a2 ) ] }
F3 = { (2Qq) / [ ( 4πεo a2 ) ] }
By equating FR and F3 and considering q is -ve, we get q = (-Q/4) [ 2√2 + 1 ]
-----------------------------------------------------------
Qn.(2)
Force of attraction between two charges act as centripetal force , so that charge -q1 moving with speed v is in circular orbit of radius r

we get, 

Period of revolution T = ( 2πr / v ), hence we get
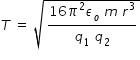
----------------------------------------------------------------------
Qn.(3)
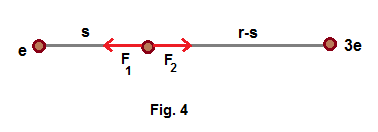
Let the point charge be placed at a distance s from charge e. Hence its distance from charge 3e is (r-s)
force F2 on unit positive charge due to charge e is given by, F2 = e / [ (4πεo ) s2 ]
force F1 on unit positive charge due to charge 3e is given by, F1 = 3e / [ (4πεo ) (r-s)2 ]
By equating F1 and F2 , we get s= r / [ √3 + 1 ]
----------------------------------------------------------------------------
Qn.(4)
reason :- Electric field will be normal at the surface of conductor
----------------------------------------------------
Qn.(5)
An electric dipole in a uniform electric field experiences maximum moment of couple
when the dipole is placed perpendicular to the direction of the field
-------------------------------------------------
Qn.(6).
Electric flux φ through hemisphere ( curved surface + base ) 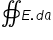
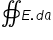
By Gauss law , we have, 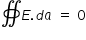 because there are no enclosed charges in hemisphere
because there are no enclosed charges in hemisphere
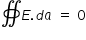 because there are no enclosed charges in hemisphere
because there are no enclosed charges in hemisphere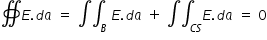
where subscript B stands for surface integral over base and subscript CS stands for surface integral over curved surface
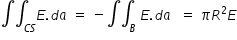
------------------------------------------------------------
Qn.(7)
Vertical displacement h of charge is given by, h = (1/2) a t2 , where a = qE/m , is acceleration experienced by charge q which is having mass m.
E is electric field intensity
hence vertical deflection, h = (1/2) (q/m) E t2
Hence vertical deflection is directly proportional to q/m . Hence particle-c has higher charge to mass ratio
------------------------------------------------------------
Qn. (8)
F = q2 / (4πεo r2 )
if q = 1 C , r = 1000 m
F = 1 × 9 × 109 × 10-6 N = 9 × 103 N
-------------------------------------------------
Qn. (9) EA > EB
reason :- at point A, field lines intensity is more ( or lines are closely spaced ) in comparison with point-B.
-----------------------------------
Qn.(10) I am not able to get proper answer
------------------------
Qn.(11) this question is not readable to me, numbers are not visible properly
------------------------
Qn.12
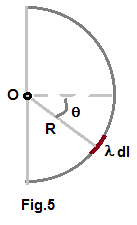
Electric field intensity E is given by

-------------------------------
Q.13
Electric lines are parallel to surface. Hence electric flux through surface is zero
--------------------------------
Q.14
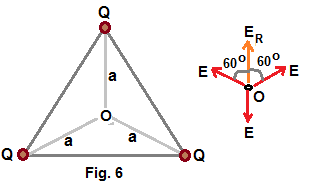
Point O is at equal distance a from all the charges.
Potential is scalar function of distance a . Hence potential due to each charge is getting added together and
total potential V = 3Q / [ (4πεo) a] ≠ 0.
Electric fields are shown in figure. Net Electric field = ER - E = 2 cos60 E - E = 0
Hence the answer :- E = 0 , V ≠ 0.
Answered by Thiyagarajan K | 29 Mar, 2020, 12:36: PM
Concept Videos
CBSE 12-science - Physics
Asked by dasrituparna1999 | 13 Apr, 2024, 06:56: AM
CBSE 12-science - Physics
Asked by dasrituparna1999 | 12 Apr, 2024, 09:26: PM
CBSE 12-science - Physics
Asked by mishrigupta19319 | 08 Apr, 2024, 06:28: PM
CBSE 12-science - Physics
Asked by madhav9119887644 | 07 Apr, 2024, 08:10: PM
CBSE 12-science - Physics
Asked by mishrigupta19319 | 07 Apr, 2024, 11:23: AM
CBSE 12-science - Physics
Asked by adityagalar2007 | 06 Apr, 2024, 01:06: PM
CBSE 12-science - Physics
Asked by amlanmcob | 06 Apr, 2024, 12:27: PM
CBSE 12-science - Physics
Asked by hussain221man | 05 Apr, 2024, 08:44: PM
CBSE 12-science - Physics
Asked by mishrigupta19319 | 05 Apr, 2024, 12:01: PM
CBSE 12-science - Physics
Asked by manishamunda787 | 02 Apr, 2024, 11:07: AM