CBSE Class 12-science Answered
Show that the relation R in the set A = {a, b, c} given by R = {(b, c), (c, b)} is symmetric but neither reflexive nor transitive.
Asked by Topperlearning User | 25 Oct, 2016, 07:53: AM
Expert Answer
(i) Since, (a, a), (b, b), (c, c)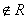
, therefore R is not reflexive.
, therefore R is not reflexive.(ii) Since, (b, c), (c, b)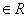
, therefore R is symmetric.
, therefore R is symmetric.(iii) There are only two elements b and c are in relation R and there is no third element a in R, so R is not transitive.
Answered by | 25 Oct, 2016, 09:53: AM
Concept Videos
-
Introduction to Relations
This video explains the concept of relations and types of relation like Emp... -
Concept of relations and types of relation
Understand the concept of relations and types of relation: - Empty Relation... -
Introduction To Relations
Understand the concept of relations and types of relation: - Empty Relatio...
CBSE 12-science - Maths
Asked by aiswaryaanil0009 | 01 Feb, 2024, 08:36: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by amandwivesh | 25 Oct, 2023, 11:57: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by rginish12 | 04 Oct, 2023, 11:14: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by iamujjy | 21 May, 2023, 04:55: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by shauryacho40 | 08 Apr, 2021, 10:48: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by majethiyarishat9566.12sdatl | 27 Oct, 2020, 11:51: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by seeni2005 | 30 Sep, 2020, 01:19: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by ksanjeev8214 | 29 Sep, 2020, 01:34: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by seeni2005 | 29 Sep, 2020, 01:08: PM
ANSWERED BY EXPERT
