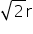CBSE Class 12-science Answered
 Also find maximum volume.
Also find maximum volume.In this question we see the radius of sphere is constant R. So we shall assume sphere is fixed. Also cylinder inside the sphere is variable. We need to find the dimensions of cylinder, which makes this of maximum volume.
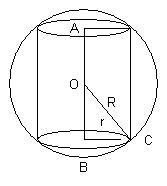 Consider the cylinder of radius r and height h so its volume becomes
Consider the cylinder of radius r and height h so its volume becomes

Now from figure AB = h so that 
So we get 
Using this the volume becomes

Assuming ![]() to be constant we differentiate with respect to
to be constant we differentiate with respect to ![]() we get
we get

For maximum or minimum value

To check whether this is a point of local maxima or minima we differentiate once again with respect to h
 which of course is negative
which of course is negative
So  is a point of maxima
is a point of maxima
Hence volume of cylinder is maximum when its height is  times the radius of outer sphere.
times the radius of outer sphere.





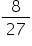 of the volume of the sphere.
of the volume of the sphere.