CBSE Class 10 Answered
show that every positive even integer is of the form 2q and that every positive integer i of the form 2q+1,where q is some integer.
Asked by FEHMEEDAH NAZNEEN | 07 Jul, 2010, 12:00: AM
Expert Answer
Dear student, following is the answer to your query:
Let a be any positive integer and b = 2.
Applying Euclid’s algorithm, we have:
a = 2q + r, for some integer q ≥ 0, and 0 ≤ r < 2
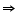a = 2q or 2q + 1
If a = 2q, then a is an even integer.
Now, a positive integer can either be even or odd. Thus, any positive odd integer is of the form 2q + 1.
Regards
TooperLearning
Answered by | 14 Jul, 2010, 02:45: PM
Application Videos
-
Relation between HCF and LCM
This video describe Relation between HCF and LCM. -
HCF of given two numbers
This video explains the Method of division algorithm to find the HCF of the... -
Word Problem based on LCM and HCF
This video explains the use of LCM and HC in solving a word problem. -
LCM and HCF
The video describes to find the HCF of two numbers
-
Relation between LCM and HCF
The video describes the relation between LCM and HCF & the numbers
Concept Videos
-
Euclid's Division Lemma and Algorithm ...
This video explains the statement of Euclid's Division lemma and algorithm ... -
Fundamental Theorem of Arithmetic ...
Determination of H.C.F and L.C.M of numbers using Prime Factorization and ... -
Rational and Irrational Numbers
Discuss rational and irrational numbers and express them on the number lin... -
Euclid's Division Lemma and Algorithm
This video explains the statement of Euclid's Division lemma and algorithm ... -
Fundamental Theorem of Arithmetic
Determination of H.C.F and L.C.M of numbers using Prime Factorization and s...
CBSE 10 - Maths
Asked by nagalaxmidurgarao937 | 08 Apr, 2024, 01:42: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by sagarmishra | 14 Mar, 2024, 12:11: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by apekshab05918 | 15 Feb, 2024, 11:29: AM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by sitalagrawal969 | 21 Jan, 2024, 11:48: AM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by bhaskrraobhaskrrao | 18 Jan, 2024, 08:35: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by randhirpandey196 | 16 Jan, 2024, 03:29: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by scs902692 | 11 Jan, 2024, 08:49: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by reddyjaswamth | 10 Jan, 2024, 01:49: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by dc5756069 | 09 Jan, 2024, 07:35: AM
ANSWERED BY EXPERT
Get in Touch
