CBSE Class 10 Answered

note that the remainder which is left after you divide any no by 6, has to be less than 6

 so if r is the remainder when a number p is divided by 6 and if q is the quotient, then we can write

 p=6q+r     where r=0 or 1 or 2 or 3 or 4 or5.

pecularity of these numbers from 0,1..5 is that when their cubes are divided by 6 then the remainder is the same as the number.For 0 there's nothing to prove. So let's start from 1.

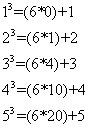
the first two terms of the expansion are divisible by 6 and the last term will leave a remainder equal to r (because r is less than 6) as shown above.

Hence whne a number p or its cube are divided by 6, they leave the same remainder r.