Show that 5+square root of 6 is irrational

Dear student

Following is the solution to your problem:

Let us assume, to the contrary, that 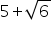      is a rational number .

So, we can find co primes a and b (b non zero) such that

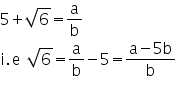
now a-5b and b are integers and b i snon zero so a-5b/b is rational.

Since Rhs is rational implies 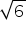is r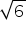ational

Which contradicts the fact that is irrational.

So our assumption is wrong and  5+ is irrational.

Hope it clarifies the doubt

Regards

Team Topperlearning