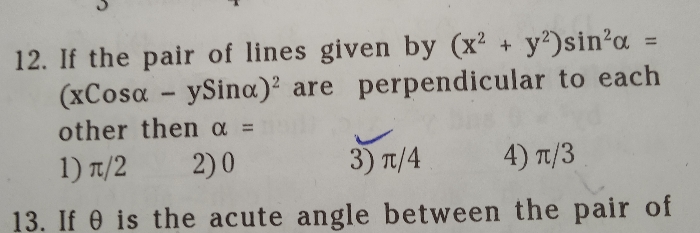CBSE Class 11-science Answered
SETS
Asked by | 28 Jun, 2008, 12:23: PM
Expert Answer
We will prove the result by principle of mathematical induction.
to show, 4n -3n -1= 9(m-1), n,m
N
for n=1
4n -3n -1=0=9x0=9(1-1). thus, result is true for n = 1
let the result be true for n = k.
this implies, 4k-3k-1 = 9(m-1) for some m in N
consider n = k+1
4k+1-3(k+1) -1
=4k.4-3k-4-12k+12k
=4(4k-3k-1)+9k
=4.9(m-1)+9k
=9(4m-4+k)
=9(p-1) where p =4m+k-3 N
hence, it is true for all n in N by principle of mathematical induction.
Answered by | 15 Jul, 2008, 11:33: AM
Application Videos
-
Relation between roots and coefficient of a Quadratic E ...
Video contains the question based on quadratic equation where the relation ... -
Sum of infinite terms of an Arithmetic-Geometric Progre ...
Video contains the question based on how to find the sum of infinite terms ... -
Introduction to Locus of a point and its equation ...
Video contains the question based on finding equation of locus of a point -
Problems based on Equation of Locus of a Point ...
Video contains the question based on finding equation of locus of a poin...
-
Introduction to Translation of Axes and Problems based ...
Video contains the question based on translation of axes
Concept Videos
-
Trigonometric identities and problems
Fundamental trigonometric identities and problems based on them. Sign Conve... -
Degree measure and Radian measure ...
This video explains the concept of negative & positive angles, conversion o... -
Types of sets and its representation
Types of sets and describe two forms of set representation. -
Subsets and Supersets
This video covers the definition of subsets and supersets of a set and also... -
Representing the union and intersection of sets
Venn diagrams. Represent the union and intersection of sets with the help o...
CBSE 11-science - Maths
Asked by sampabarman328 | 18 Apr, 2024, 01:20: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by tahikpreet0001 | 17 Apr, 2024, 06:41: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by nitinkrjsr07082008 | 15 Apr, 2024, 11:32: PM
ANSWERED BY EXPERT
CBSE 11-science - Maths
Asked by kanhaparashar17 | 04 Apr, 2024, 12:55: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by dseno1741 | 29 Mar, 2024, 08:47: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by parvanipatil09 | 29 Mar, 2024, 10:12: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by rishithatelaprolu84 | 29 Mar, 2024, 08:32: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by Manjeet | 23 Mar, 2024, 09:41: PM
ANSWERED BY EXPERT
