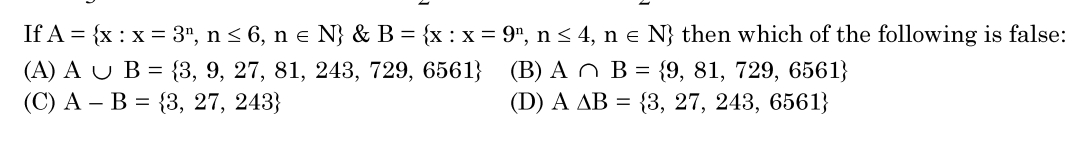CBSE Class 11-science Answered
SETS
Asked by | 28 Jun, 2008, 12:15: PM
For A =B A B and B
B and B A
A
 B and B
B and B A
A For A B
B
 B
B Let a be an element in A.
To show: ‘a B
B
a A⇒a
A⇒a  A
A X = B
X = B X (given)
X (given)
a  B
B X
X
a B or a
B or a X if a
X if a B then A
B then A B
B
If a X and as a
X and as a A then a
A then a A
A  X = B
X = B X = Φ
X = Φ
 B
B X
Xa
 B or a
B or a X if a
X if a B then A
B then A B
B If a
 X and as a
X and as a A then a
A then a A
A  X = B
X = B X = Φ
X = Φ using the intersection properties
So a cannot be in X
hence A B
B
 B
B Similarly by the symmetric argument B A
A
 A
A
Answered by | 30 Jun, 2008, 10:15: AM
Concept Videos
CBSE 11-science - Maths
Asked by parvanipatil09 | 29 Mar, 2024, 10:12: AM
CBSE 11-science - Maths
Asked by divyanshtikkiwal6 | 23 Feb, 2024, 07:44: PM
CBSE 11-science - Maths
Asked by pranavsrinivas82 | 14 Jan, 2024, 07:45: AM
CBSE 11-science - Maths
Asked by pranavsrinivas82 | 10 Jan, 2024, 08:45: PM
CBSE 11-science - Maths
Asked by naiduuofficial | 06 Jan, 2023, 07:49: PM
CBSE 11-science - Maths
Asked by anjaneyagadgil04 | 05 Jan, 2023, 12:16: PM
CBSE 11-science - Maths
Asked by bangtan7hybe | 18 Sep, 2022, 06:36: PM
CBSE 11-science - Maths
Asked by kdimple765 | 24 Jun, 2022, 04:22: PM
CBSE 11-science - Maths
Asked by arjunsah797 | 03 Mar, 2022, 06:04: PM
CBSE 11-science - Maths
Asked by krishkhare04 | 03 Feb, 2022, 02:35: PM