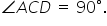CBSE Class 10 Answered
S AND T trisect the side QR of a right triangle PQR. Prove that 8PT2=3PR2+5PS2
Asked by apporv1999 | 07 Jul, 2014, 09:32: PM

Since, S and T trisect the side QR
QS = TS = RT
Let’s assume QS = TS = RT = x
QR = 3x and QT = 2x
In Right angled triangle PQR,
PR2 = PQ2 + QR2
PR2 = PQ2 +(3x)2
PR2 = PQ2 + 9x2
In Right angled triangle PQS,
PS2 = PQ2 +QS2
PS2 = PQ2 +x2
In Right angled triangle PQT,
PT2 = PQ2 + OT2
PT2 = PQ2 + (2x)2
PT2 = PQ2 + 4x2
To prove that, 8PT2 =3 PR2 + 5PS2
LHS = 8PT2 = 8(PQ2 + 4x2) = 8PQ2 + 32x2
RHS = 3 PR2 + 5PS2 = 3(PQ2 + 9x2) – 5 (PQ2 + x2)= 3PQ2 + 27x2 + 5PQ2 + 5x2 = 8PQ2 + 32x2
LHS = RHS
Hence, proved
Answered by Anuja Salunke | 08 Jul, 2014, 11:14: AM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by deepak13376 | 23 Sep, 2020, 01:33: PM
CBSE 10 - Maths
Asked by rhtwatts | 06 Mar, 2019, 03:59: PM
CBSE 10 - Maths
Asked by Topperlearning User | 26 Jul, 2017, 01:58: PM
CBSE 10 - Maths
Asked by Topperlearning User | 26 Jul, 2017, 01:58: PM
CBSE 10 - Maths
Asked by Topperlearning User | 26 Jul, 2017, 01:58: PM
CBSE 10 - Maths
Asked by Topperlearning User | 26 Jul, 2017, 01:58: PM
CBSE 10 - Maths
Asked by Topperlearning User | 26 Jul, 2017, 01:58: PM
CBSE 10 - Maths
Asked by Topperlearning User | 05 Dec, 2013, 08:56: AM
CBSE 10 - Maths
Asked by Topperlearning User | 26 Jul, 2017, 01:58: PM




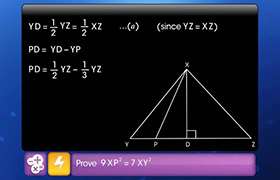

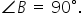 If AD2 = AB2 + BC2 + CD2. Prove that
If AD2 = AB2 + BC2 + CD2. Prove that