CBSE Class 12-science Answered
R is a relation on a set N of natural numbers defined by
R={(x,y): y = nx , n  N} check whether R is reflexive, symmetric and transitive.
N} check whether R is reflexive, symmetric and transitive.
 N} check whether R is reflexive, symmetric and transitive.
N} check whether R is reflexive, symmetric and transitive.
Asked by fleurnym | 03 May, 2020, 04:50: PM
Given relation is R={(x,y): y = nx , n  N}
N}
 N}
N}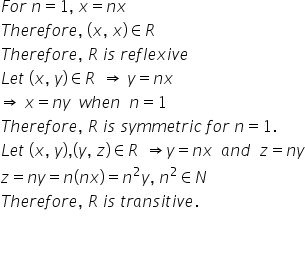
Answered by Renu Varma | 03 May, 2020, 10:58: PM
Concept Videos
CBSE 12-science - Maths
Asked by aiswaryaanil0009 | 01 Feb, 2024, 08:36: PM
CBSE 12-science - Maths
Asked by amandwivesh | 25 Oct, 2023, 11:57: PM
CBSE 12-science - Maths
Asked by rginish12 | 04 Oct, 2023, 11:14: AM
CBSE 12-science - Maths
Asked by iamujjy | 21 May, 2023, 04:55: PM
CBSE 12-science - Maths
Asked by shauryacho40 | 08 Apr, 2021, 10:48: AM
CBSE 12-science - Maths
Asked by majethiyarishat9566.12sdatl | 27 Oct, 2020, 11:51: AM
CBSE 12-science - Maths
Asked by seeni2005 | 30 Sep, 2020, 01:19: PM
CBSE 12-science - Maths
Asked by ksanjeev8214 | 29 Sep, 2020, 01:34: PM
CBSE 12-science - Maths
Asked by seeni2005 | 29 Sep, 2020, 01:08: PM







