CBSE Class 9 Answered
Q1. Prove that the quadrilateral formed by the internal angle bisectors of any quadrilateral is cyclic ?
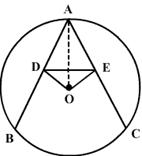
Q2. AB is a diametre of the circle ,CD is a chord equal to radius of the circles ,AC and BD when extended intersect at point E. Prove that angle AEB=60 ?
Q3. A chord of a circle is equal to radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on a major arc ?
Q4. If the non-parallel sides of a trapezium are equal ,prove it is cyclic ?
Asked by shub3893 | 03 Dec, 2015, 08:56: PM
Please post one question in a single post.
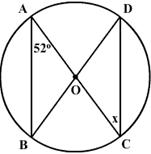
The explanation for Q2 is given below:
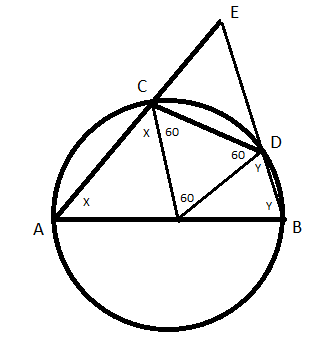
The circle is shown in the figure above.
Let the center be point 'O'.
OC=OD=CD (since CD is equal to radius)
So OCD is an equilateral triangle. Each angle of the triangle COD is 60 degree.
The angle shown by 'X, X' and 'Y,Y' form isosceles triangles.
Now ABDC is a cyclic quadrilateral. So angle B + angle C = 180 degree
Y + 60+X = 180
X+Y = 120 degree
In the triangle AEB, X + Y + angle (AEB) = 180
120 + angle (AEB) = 180
angle (AEB) = 60 degree
Answered by satyajit samal | 04 Dec, 2015, 12:19: PM
Concept Videos
CBSE 9 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 9 - Maths
Asked by Topperlearning User | 05 Oct, 2017, 08:15: AM
CBSE 9 - Maths
Asked by Topperlearning User | 18 Aug, 2017, 08:51: AM
CBSE 9 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 9 - Maths
Asked by Topperlearning User | 05 Oct, 2017, 08:17: AM
CBSE 9 - Maths
Asked by Topperlearning User | 05 Oct, 2017, 08:25: AM
CBSE 9 - Maths
Asked by Topperlearning User | 18 Aug, 2017, 08:49: AM
CBSE 9 - Maths
Asked by Topperlearning User | 05 Oct, 2017, 08:22: AM
CBSE 9 - Maths
Asked by Topperlearning User | 18 Aug, 2017, 08:40: AM
CBSE 9 - Maths
Asked by Topperlearning User | 05 Oct, 2017, 08:24: AM





 XPZ is equal to twice the sum of
XPZ is equal to twice the sum of 
 ADE is an isosceles triangle.
ADE is an isosceles triangle.