Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

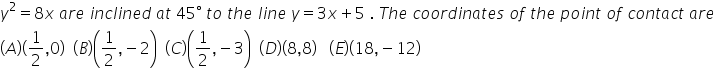
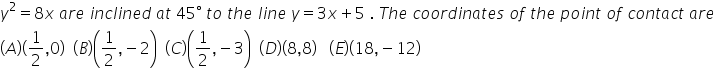
Q)Tangents to y squared equals 8 x space a r e space i n c l i n e d space a t space 45 degree space t o space t h e space l i n e space y equals 3 x plus 5 space. space T h e space c o o r d i n a t e s space o f space t h e space p o i n t space o f space c o n t a c t space a r e left parenthesis A right parenthesis left parenthesis 1 half comma 0 right parenthesis space space left parenthesis B right parenthesis open parentheses 1 half comma negative 2 close parentheses space space left parenthesis C right parenthesis open parentheses 1 half comma negative 3 close parentheses space space left parenthesis D right parenthesis open parentheses 8 comma 8 close parentheses space space space left parenthesis E right parenthesis open parentheses 18 comma negative 12 close parentheses
Asked by araima2001 | 24 Mar, 2017, 07:31: PM
answered-by-expert Expert Answer
begin mathsize 16px style Given space that space tangents space to space straight y squared equals 8 space straight x space are space inclined space at space 45 degree space to space the space line space straight y space equals space 3 straight x plus 5. Using space the space slope space formula comma tanθ equals open vertical bar fraction numerator straight m subscript 1 minus straight m subscript 2 over denominator 1 plus straight m subscript 1 straight m subscript 2 end fraction close vertical bar rightwards double arrow tan 45 equals open vertical bar fraction numerator straight m minus 3 over denominator 1 plus 3 straight m end fraction close vertical bar rightwards double arrow 1 equals open vertical bar fraction numerator straight m minus 3 over denominator 1 plus 3 straight m end fraction close vertical bar rightwards double arrow fraction numerator straight m minus 3 over denominator 1 plus 3 straight m end fraction equals plus-or-minus 1 space rightwards double arrow fraction numerator straight m minus 3 over denominator 1 plus 3 straight m end fraction equals 1 space space or space space fraction numerator straight m minus 3 over denominator 1 plus 3 straight m end fraction equals negative 1 rightwards double arrow straight m minus 3 equals 1 plus 3 straight m space or space straight m minus 3 equals negative 1 minus 3 straight m rightwards double arrow 2 straight m equals negative 4 space space or space 4 straight m equals 2 rightwards double arrow straight m equals negative 2 space or space straight m equals 1 half Equation space of space the space tangent space with space slope space straight m equals negative 2 space or space straight m equals 1 half space to space the space parabola space is space given space by straight y equals mx plus straight a over straight x space where space the space equation space of space teh space parabola space is space given space by space straight y squared equals 4 ax In space this space case space straight a equals 2 comma space straight m equals negative 2 space or space straight m equals 1 half So comma space the space equation space of space the space tangents space are space straight y equals negative 2 straight x minus 1 space and space straight y equals 1 half straight x plus 4. Now space to space find space the space coordinates space of space the space point space of space contact space of space the space tangents comma solve space the space equation space of space the space tangents space and space the space parabola space simultaneously. For space the space tangent space straight y equals negative 2 straight x minus 1 space and space space straight y squared equals 8 straight x comma you space will space get space straight y equals 1 half space and space straight x equals negative 2 For space the space tangent space straight y equals 1 half straight x plus 4 space and space space straight y squared equals 8 straight x comma you space will space get space straight y equals 8 space and space straight x equals 8 So comma space the space points space would space be space open parentheses 1 half comma negative 2 close parentheses space and space left parenthesis 8 comma 8 right parenthesis. end style
Answered by Rebecca Fernandes | 24 Mar, 2017, 10:54: PM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Maths
construction of Parabola When Distance between directrix and focus is given
Asked by praveenaditya843 | 22 Dec, 2023, 10:41: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
If PSQ is the focal chord of the parabola y^2=8x such that SP=6 then the length of SQ is  1)3 2)4 3)24
Asked by dineshchem108 | 21 Oct, 2018, 07:54: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the vertex, focus, axis, diectrix x and latus rectum of the parabola.(a) y2 = 8x(b)y2 = -12x (c) x2 = 4y and (d) x2 = -16y.
Asked by Topperlearning User | 27 Feb, 2015, 01:28: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the equation of the parabola whose focus is (3,0) and the vertex is (0.0).
Asked by Topperlearning User | 13 Nov, 2016, 05:55: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the equation of the parabola whose focus is (4,0) and the directix x = -4.
Asked by Topperlearning User | 30 Apr, 2014, 11:27: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the equation of the parabola with vertex (0,0) and focus (-5,0).
Asked by Topperlearning User | 30 Apr, 2014, 11:28: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the equation of the parabola with V(0,0) and focus (0,-2).
Asked by Topperlearning User | 30 Apr, 2014, 11:29: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the equation of the parabola with focus (0,4) and directix y = -4.
Asked by Topperlearning User | 30 Apr, 2014, 11:29: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the equation of the parabola whose focus is (0,-7) and vertex is (0,0) 
Asked by Topperlearning User | 13 Nov, 2016, 05:54: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the equation of the parabola with vertex (0,0), passing through the point (4,5) and symmetric about the x - axis.
Asked by Topperlearning User | 27 Feb, 2015, 01:20: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×