Q. Prove that the points A,B,C,D are concyclic if the line segments AB and CD intersect at a point P such that AP.PB = CP.PD

 

Construction: Draw the circle through the three non – collinear points A, B, C. 

This is possible, according to the theorem that 'A circle always passes through three non-collinear points'.

If D lies on this circle, then the result follows.

A, B, C and D are concyclic.

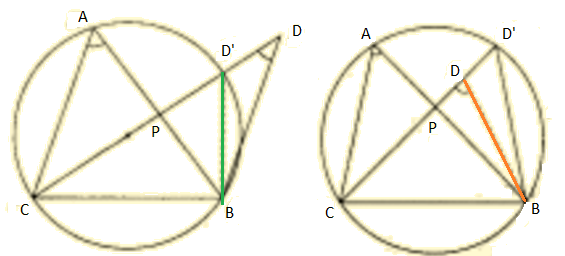
If possible, suppose D does not lie on this circle. Then, this circle will intersect CD at D’. Join D'B.

So, AP.PB = CP.PD'

But we are given that AP.PB = CP.PD.

D' coincides with D.

D lies on the circle passing through A, B and C.

Hence, the points A, B, C and D are concyclic.