Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 9 Answered

Q) In the figure,AB=AC,D is the point in the interior of triangle ABC such that angle DBC=angle DCB. Prove that AD bisects angle BAC of triangle ABC.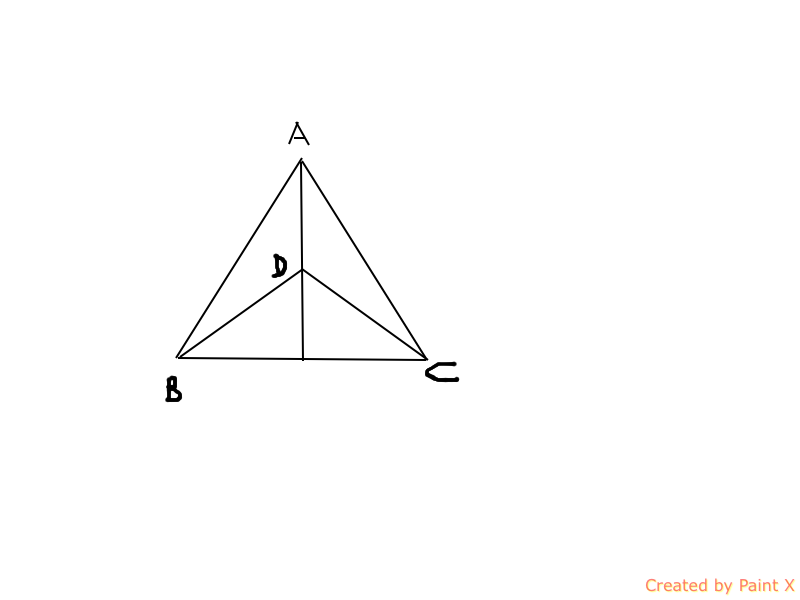
Asked by banerjee_milky | 27 Jun, 2017, 07:51: PM
answered-by-expert Expert Answer
begin mathsize 16px style Given space that space AB equals AC space and space angle DBC equals angle DCB. To space prove colon space AD space bisects space angle straight A SInce space angle DBC equals angle DCB So comma space DB equals DC space space.... left parenthesis sides space opposite space equal space angles space are space equal right parenthesis space space space space space space space.... left parenthesis straight i right parenthesis In space triangle ABD space and space triangle ACD comma AB equals AC space space.... left parenthesis Given right parenthesis AD equals AD space space.... left parenthesis Common space side right parenthesis DB equals DC space space.... left parenthesis from space left parenthesis straight i right parenthesis right parenthesis So comma space triangle ABD approximately equal to triangle ACD space space.... left parenthesis SSS space congruence space criterion right parenthesis rightwards double arrow angle BAD equals angle CAD space space.... left parenthesis cpct right parenthesis That space is comma space AD space bisects space angle BAC. end style
Answered by Rebecca | 28 Jun, 2017, 09:34: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 9 - Maths
triangle ABC is an equilateral triangle, AB = 6cm. the points P,Q and R are midpoints of AB BC, CA respectively . the perimeter of □ PBCR is
question image
Asked by ghodage | 12 Dec, 2023, 07:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
the area of an equilateral triangle is 49√3 sq.cm, it's perimeter is
Asked by vijaykasaudhan913 | 10 Dec, 2023, 04:40: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
M is a point inside a square ABCD. AMCD is equilateral triangle and MC cuts diagonal DB at E. Then, ZBEC=..... (1) 75° (3) 105° (2) 90° (4) 60°
Asked by Krishna962511 | 23 Jan, 2023, 10:41: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
In fig. 12.116 , T is a point on the side QR of ∆ PQR and S is a point such that RT=St. Prove that PQ+PR>QS
Asked by shivendrasinghfauzdar | 09 Oct, 2021, 11:30: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
In the figure, ABCD is a square and PAB is a triangle such that AQ = BR. Prove that DPQR is an isosceles triangle.
Asked by thebeatinbrat | 01 Oct, 2021, 08:56: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
If the vertex angle of an isosceles triangle is 50° ,find the other angels   
Asked by chikkammac24212 | 21 Aug, 2019, 07:48: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
show that BX=CY.
question image
Asked by shubham0kumar24 | 19 May, 2019, 12:44: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
AD is an altitude of an isosceles triangle ABC in which AB=AC.Show that  ( i )AD bisects BC (ii) AD bisects angle A.
Asked by Nagu.sahukar1543 | 14 Nov, 2018, 08:11: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
If the segments drawn perpendicular to the two sides of a triangle from the mid point of the third side be congruent and equally inclined to the third side, prove that the triangle is isosceles.
Asked by Topperlearning User | 10 Aug, 2017, 01:53: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
If the altitudes from two vertices of a triangle to the opposite sides are equal, prove that the triangle is isosceles.
Asked by Topperlearning User | 10 Aug, 2017, 01:56: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×