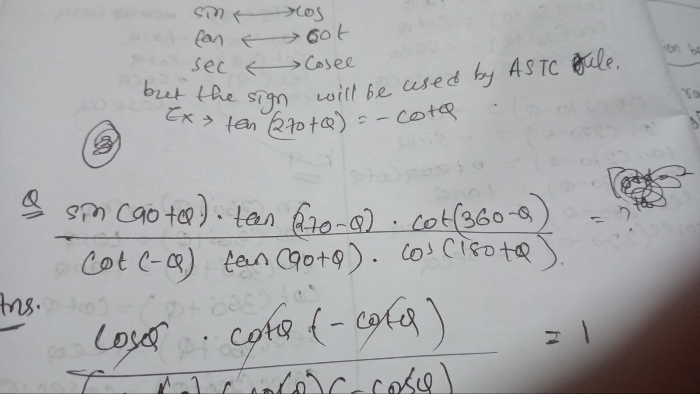let B be the aero plane
D be the image
AC be y
BC be x
BC = h-x
CD = a + h
Consider ABC
Sin alpha = h-a / y
Y=h-a/ Sin alpha ------------ (1)
Consider ACD
Sin beta = h + a / y
Y= Sin beta / h + a ------------ (2)
From (1) & (2)
h-a/ Sin alpha = Sin beta / h + a
h-a (Sin beta) = h + a (Sin alpha)
h Sin beta-a Sin beta = h Sin alpha +a Sin alpha
h (Sin beta- Sin alpha) = a (Sin alpha - Sin beta)
h=a sin (alpha + beta) / sin (beta - alpha)
hence proved
CBSE Class 11-science Answered
Q:-from the top of a tree on the bank of a lake , an aeroplane in the sky makes an angle of elevation or and its image in the river makes an angle of depression .if the height of the tree from the water surface is 'a' and the height of the aeroplane is 'h'. show that h=asin(a+b)/sin(b-a)
Asked by Bharadwaj.R.S | 01 Feb, 2011, 12:00: AM
Expert Answer
Answered by | 07 Feb, 2011, 10:14: AM
Concept Videos
-
Trigonometric identities and problems
Fundamental trigonometric identities and problems based on them. Sign Conve... -
Degree measure and Radian measure ...
This video explains the concept of negative & positive angles, conversion o... -
Domain, period and range of trigonometric functions ...
Define the domain, period and range of the trigonometric functions and plot... -
Basic Trigonometric Formulae
Derive and apply the basic formulae of sine and cosine functions like sin(... -
Sign of Trigonometric Functions
This video covers values of trigonometric ratios of angles greater than 90 ...
CBSE 11-science - Maths
Asked by rajyothi64 | 05 Mar, 2024, 09:49: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by ghoshshawata62 | 04 Mar, 2024, 08:16: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by nayaktapaswini2007 | 29 Feb, 2024, 09:10: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by bimanmandal53361 | 15 Jan, 2024, 12:32: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by sreyas.katuri | 23 Sep, 2023, 07:12: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by 069.pks | 16 Sep, 2023, 10:06: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by surekhashriwas01 | 12 Sep, 2023, 08:39: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by mvr23467 | 12 Sep, 2023, 07:52: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by SasipriyaNagappan | 27 Jul, 2023, 07:22: PM
ANSWERED BY EXPERT
