Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

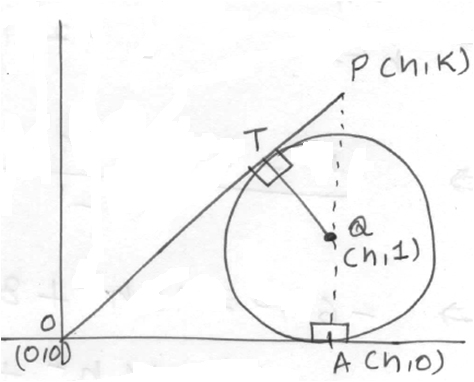
Q) A circle S , whose radius is 1 unit, touches the X axis at point A. The center Q of S lies in the first quadrant . The tangent from the origin O to the circle touches it at T & a point P lies on it such that the triangle  OAP is a right angled triangle at A & its perimeter is 8 unit. then the length of QP is:
(A)2   (B)1/2    (C)4/3   (D)5/3
Asked by araima2001 | 29 Dec, 2016, 11:01: PM
answered-by-expert Expert Answer
begin mathsize 16px style Given space that space radius space equals space 1 space unit space and space that space straight S space touches space the space straight x minus axis space at space straight A space where space say space straight A identical to left parenthesis straight h comma 0 right parenthesis So comma space centre space straight Q identical to left parenthesis straight h comma 1 right parenthesis Since space increment OAP space is space straight a space right space triangle space with space PA space perpendicular OA rightwards double arrow straight P identical to left parenthesis straight h comma straight k right parenthesis space... left parenthesis Supposing space its space straight Y minus coordinate space is space straight k right parenthesis Again space in space increment OAP comma OA space equals space straight h comma space PA space equals space straight k space rightwards double arrow OP equals square root of straight h squared plus straight k squared end root As space OP space and space straight X minus axis space space are space tangents space to space straight S comma space with space straight T space and space straight A space being space points space of space tangency comma space OT equals OA equals straight h space units space.... left square bracket Since space straight a space pair space of space tangents space to space the space same space circle space are space equal space in space lengths right square bracket rightwards double arrow PT equals OP minus OT equals square root of straight h squared plus straight k squared end root minus straight h Now comma space in space increment QTP comma QT equals 1 space.... left parenthesis Radius space of space straight S right parenthesis QP equals AP minus AQ equals straight k minus 1 Applying space Pythagoras space theorem comma PQ squared equals PT squared plus QT squared rightwards double arrow left parenthesis straight k minus 1 right parenthesis squared equals open square brackets square root of straight h squared plus straight k squared end root minus straight h close square brackets squared plus 1 squared rightwards double arrow straight k squared plus 1 minus 2 straight k equals straight h squared plus straight k squared plus straight h squared minus 2 straight h open parentheses square root of straight h squared plus straight k squared end root close parentheses plus 1 rightwards double arrow straight h squared open parentheses square root of straight h squared plus straight k squared end root close parentheses equals straight h squared plus straight k rightwards double arrow straight h squared open parentheses straight h squared plus straight k squared close parentheses equals straight h to the power of 4 plus straight k squared plus 2 straight h squared straight k space.... left square bracket Squaring space both space sides right square bracket rightwards double arrow straight h to the power of 4 plus straight h squared straight k squared equals straight h to the power of 4 plus straight k squared plus 2 straight h squared straight k space rightwards double arrow straight k left parenthesis straight h squared minus 1 right parenthesis equals 2 straight h squared straight k rightwards double arrow straight k equals fraction numerator 2 straight h squared over denominator straight h squared minus 1 end fraction Now space as space given space perimeter space of space increment OAP equals 8 space units rightwards double arrow OP plus OA plus AP equals 8 rightwards double arrow square root of straight h squared plus straight k squared end root plus straight h plus straight k equals 8 Rearranging space and space squaring space both space sides straight h squared plus straight k squared equals left square bracket 8 minus left parenthesis straight h plus straight k right parenthesis right square bracket squared straight h squared plus straight k squared equals 64 plus straight h squared plus straight k squared plus 2 hk minus 16 left parenthesis straight h plus straight k right parenthesis rightwards double arrow fraction numerator 2 straight h cubed over denominator straight h squared minus 1 end fraction minus 8 open square brackets fraction numerator 2 straight h squared over denominator straight h squared minus 1 end fraction plus straight h close square brackets plus 32 equals 0 rightwards double arrow fraction numerator 2 straight h cubed minus 8 straight h cubed minus 16 straight h squared plus 8 straight h plus 32 straight h squared minus 32 over denominator straight h squared minus 1 end fraction equals 0 rightwards double arrow negative 6 straight h cubed minus 16 straight h squared plus 8 straight h plus 32 straight h squared minus 32 equals 0 rightwards double arrow negative 6 straight h cubed minus 16 straight h squared plus 8 straight h minus 32 equals 0 rightwards double arrow 3 straight h cubed minus 8 straight h squared minus 4 straight h plus 16 equals 0 space space space satisfies space for space straight h equals 2 Since space straight k equals fraction numerator 2 straight h squared over denominator straight h squared minus 1 end fraction PA equals 8 over 3 space space space.... left parenthesis Since space PA equals straight k right parenthesis QP equals PA minus QA space space... left parenthesis as space QA equals radius equals 1 right parenthesis QP equals 8 over 3 minus 1 rightwards double arrow QP equals 5 over 3 end style
Answered by Rebecca Fernandes | 31 Dec, 2016, 06:22: PM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Maths
2 one
question image
Asked by dra | 24 Feb, 2024, 06:35: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
construction of Parabola When Distance between directrix and focus is given
Asked by praveenaditya843 | 22 Dec, 2023, 10:41: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
To construct Different types of conic sections
question image
Asked by praveenaditya843 | 21 Dec, 2023, 07:39: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
find the coordinates of the centre of a circle passing through the points(0,0),(-2,1)and(-3,2).also , find its radius .
question image
Asked by shakyajayprakash2006 | 08 Jun, 2022, 05:26: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Examine whether the point (4, 5) lies outside or inside the circle of equation x^2+y^2-2x-3=0
Asked by sbipo2000 | 23 Feb, 2020, 03:43: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
SIR PLEASE HELP ME WITH THIS QUESTIONS : 1. Find the equation of the tangent to the circle x^2+y^2=16 drawn from the point (1,4). 2. How many triangles can be formed by joining any 3 of the 9 points when i) no 3 of them  are collinear? ii) 5 of them are collinear? 3. AB is a line of fixed length, 6 units, joining the points A(t,0) and B which lies on thepositive y axis. P is a point on AB distant 2 units from A. Express the coordinates of B and P in terms of t. Find the locus of P as t varies. 4. In a triangle ABC, (b^2 - c^2) / (b^2 + c^2) = sin(B - C) / sin(B + C), prove that it is either a right-angled or isoceles triangle.
Asked by kandappan | 08 Feb, 2020, 11:29: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
6
question image
Asked by gauravmore604 | 04 Nov, 2019, 03:31: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
The locus of point for which sum of the squares of distances from cordinate axes is 25 is
Asked by Tejravi969 | 19 Aug, 2019, 06:08: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the equation of the ellipse with centre at the origin , major axis on the x- axis and passing through the point (4,3) and (-1,4)..
Asked by Praktu111 | 09 Jun, 2019, 08:18: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
A stadium is in circular shape. Within the stadium some areas have been allotted for a hockey court and a javelin range, as given in the figure. Assume the shape of the hockey court and the javelin range to be square and triangle, resp. The curators would like to accommodate a few more sports in the stadium. Help them by measuring the unallocated region within the stadium.(the radius of the stadium is 200 mts.)  
Asked by rushabh1234 | 23 Jan, 2019, 08:59: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×