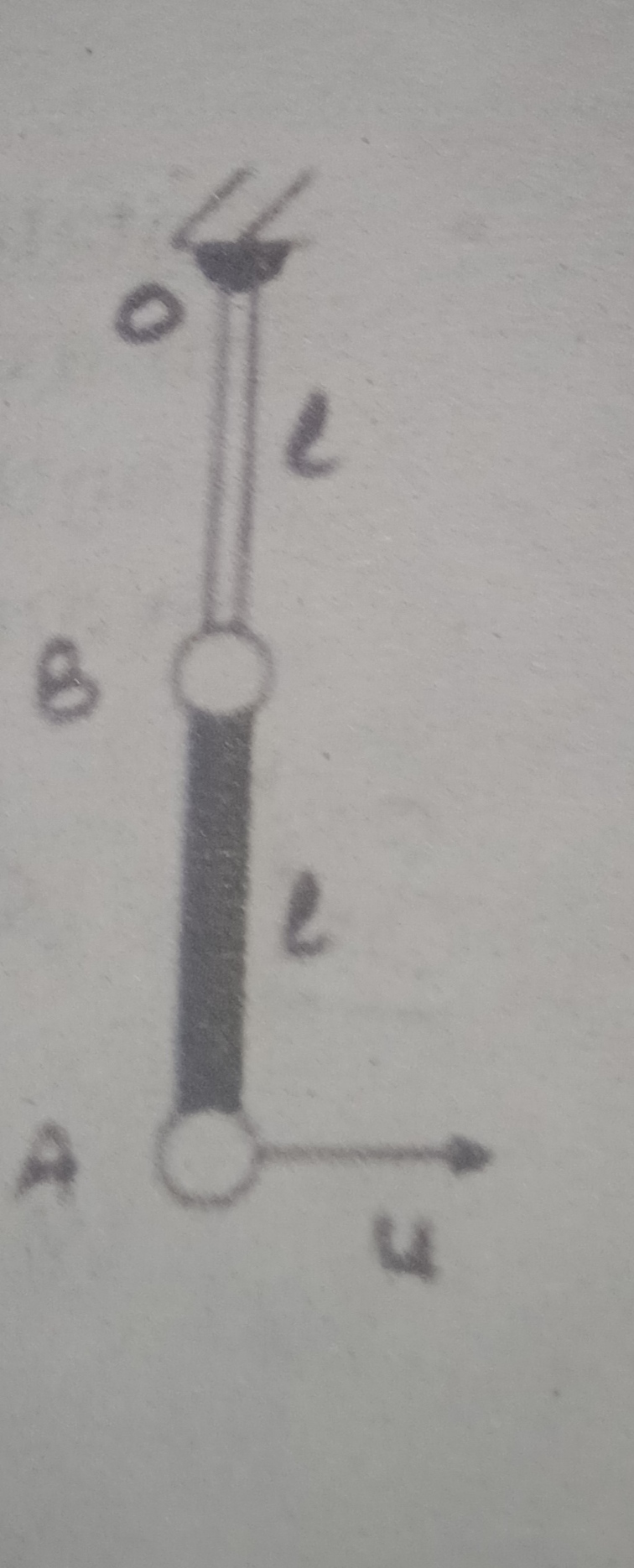Q - 19

if proton enters in magnetic field at an angle 60^o with respect to magnetic field direction  and velocity magnitude of proton is v ,

 

then resolved componet of velocity ( v sin60) perpendicular to magnetic field direction makes the proton in circular path whereas

 

the parallel component ( v cos60) makes the proton to move along the magnetic field direction resulting a helical path for proton.

 

Radius R of circular path is obtained from ,  ( m v² sin²60) / R  = ( q B v sin60 )    or  R = ( m v sin60) / ( q B )

 

where m = mass of proton, q is charge of proton and B is magnetic field induction

 

Hence Radius of circular path , R = ( 1.673 × 10^-27 × 4 × 10⁵ × 0.866 ) / ( 1.602 × 10^-19 × 0.3 ) 

 

R = 12.06 × 10^-3 m = 12.06 mm

 

Period of revolution T = ( 2π R ) / ( v sin60 )

 

In one period of revolution, proton moves a distance d along the magnetic field direction as ,

 

d = vcos60 × T  = ( 2π R ) / ( tan60 ) = ( 2π × 12.06 × 10^-3 ) / tan60 = 43.75 × 10^-3 m = 43.75 mm

 

Radius R of helical path = 12.06 mm

 

Pitch d of helical path = 43.75 mm