CBSE Class 12-science Answered
Prove that 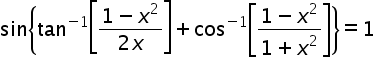
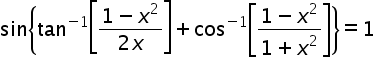
Asked by sunil2791 | 21 Apr, 2017, 07:31: PM
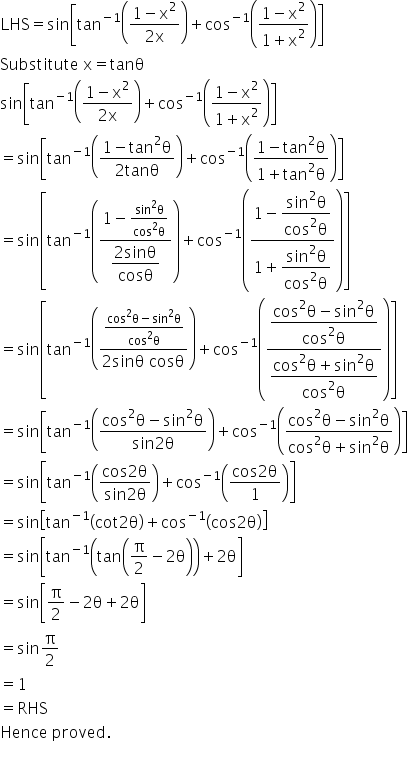
Answered by Rebecca Fernandes | 27 Nov, 2017, 12:43: PM
Concept Videos
CBSE 12-science - Maths
Asked by sahrudadayajena | 27 Jan, 2024, 09:11: PM
CBSE 12-science - Maths
Asked by rajashekararishu | 05 Jan, 2024, 09:31: PM
CBSE 12-science - Maths
Asked by ambigamagendran256 | 04 Nov, 2023, 05:43: AM
CBSE 12-science - Maths
Asked by gopalkumarrai87 | 11 Oct, 2023, 11:02: AM
CBSE 12-science - Maths
Asked by sdmbotch1123 | 10 Apr, 2023, 10:55: PM
CBSE 12-science - Maths
Asked by varma.renu9481 | 13 Mar, 2023, 11:51: AM
CBSE 12-science - Maths
Asked by w3ctiger | 12 Feb, 2023, 11:55: AM
CBSE 12-science - Maths
Asked by joymaibam38 | 26 Dec, 2021, 09:04: AM
CBSE 12-science - Maths
Asked by amansharma08116 | 14 Jul, 2021, 09:37: AM










