CBSE Class 10 Answered

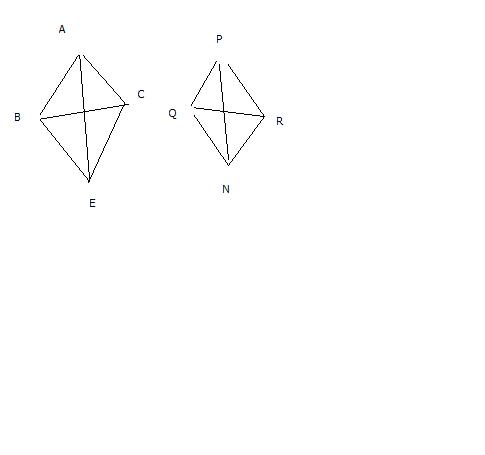
You need to do a construction here: Produce AD to E such that AD = De and produce PM to N such that PM = MN. Now join BE, CE, QN , RN.

Proof:

The two quadrilaterals formed will be parallelograms because diagonals bisect.

Now consider Triangles ABE and PQN.

AC = BE and PR = QN. AE = 2 AD and PN = 2 PM.

So, AB/PQ  =  BE/ QN  =  AE / PN

So Triangles ABE and PQN are similar

So angle BAE = angle QPN  ...(1)

similarly angle CAE = angle RPN...(2)

Adding (1) and (2) , we get

angle BAN = angle QPR .

Now by SAS similarity condition

triangle ABC is similar to triangle to triangle PQR.