ICSE Class 9 Answered
Prove that the sum of the distances of any point,within a triangle,from its vertices is less than the perimeter of the triangle.
Asked by Sushant Kumar | 03 Oct, 2013, 05:15: PM
Expert Answer
We would request you to cross check the question posted. The correct question should be:
Prove that the sum of the distances of any point,within a triangle from its vertices is greater than the perimeter of the triangle.
The proof is as follows:
The sum of any two sides of a triangle is always greater than the third side.
In OXY, OX + OY > XY ... (1)
In OYZ, OY + OZ > YZ ... (2)
In OXZ, OX + OZ > XZ ... (3)
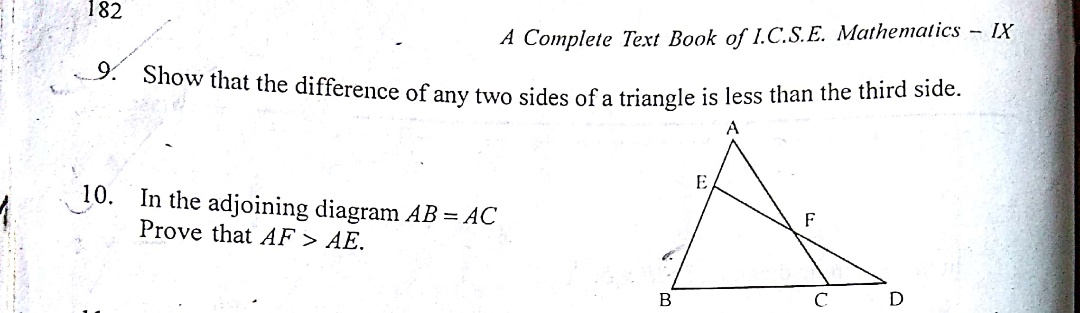
Adding equations (1), (2) and (3):
(OX + OY) + (OY + OZ) + (OX + OZ) > XY + YZ + ZX
2(OX + OY + OZ) > XY + YZ + ZX
OX + OY + OZ > (XY + YZ + ZX)
OX + OY + OZ > Semi-perimeter of XYZ > perimeter of XYZ
Hence, (OX + OY + OZ) cannot be less than the perimeter of XYZ.
Answered by | 03 Oct, 2013, 10:26: PM
Concept Videos
-
Relation between the sides and angles of a triangle ...
Relation between the length and measure of its opposite angle in a triangle... -
Inequalities in a Triangle
This video explains the relationship between the length and measure of its ... -
More on relation between sides and angles in a triangle ...
Relation between the length and measure of its opposite angle in a triangle...
ICSE 9 - Maths
Asked by sonalagarwalagarwal544 | 03 Jun, 2021, 08:34: AM
ANSWERED BY EXPERTICSE 9 - Maths
Asked by Sharmakiran | 08 Oct, 2019, 06:28: PM
ANSWERED BY EXPERT
