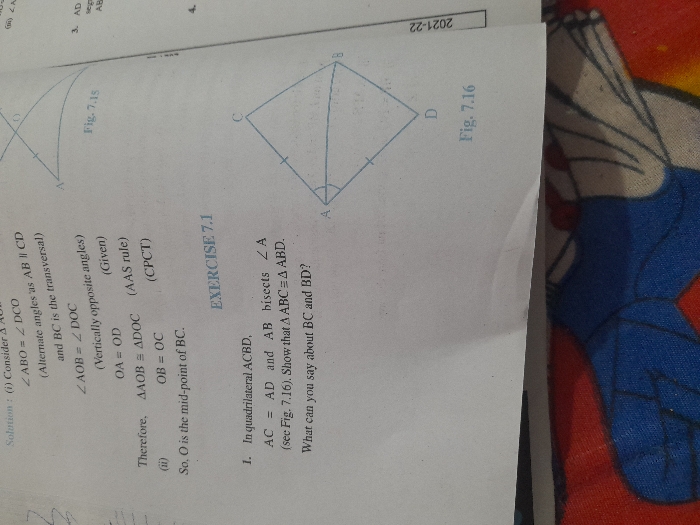
CBSE Class 9 Answered
Prove that the midpoint of hypotenuse of right angle triangle is equidistant from three vertices
Asked by sachin0706 | 22 Mar, 2009, 06:50: PM
Expert Answer
Let P be the mid point of the hypo. of the right triangle ABC, right angled at B.
Draw a line parallel to BC from P meeting AB at D.
Join PB.
in triangles,PAD and PBD,
angle PDA= angle PDB (90 each due to conv of mid point theorem)
PD=PD(common)
AD=DB( as D is mid point of AB)
so triangles PAD and PBD are congruent by SAS rule.
PA=PB(C.P.C.T.)
but
PA=PC(given as P is mid point )
So,
PA=PC=PB
Answered by | 28 Nov, 2017, 02:51: PM
Concept Videos
-
Congruence Criteria: SAS and ASA
This video explains the congruence criteria of triangles through SAS and AS... -
Congruence of geometrical figures
Congruence of geometrical figures. Establish the congruence criteria of tri... -
Congruence Criteria: SAS and ASA ...
Congruence of geometrical figures. Establish the congruence criteria of tr...
CBSE 9 - Maths
Asked by borakartike2 | 29 Dec, 2023, 09:21: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by aksharapatni | 30 Nov, 2023, 01:12: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
Asked by bathinisampath | 05 Apr, 2022, 10:50: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by abdulsamad82007 | 15 Jun, 2021, 12:59: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by rjaat7623 | 28 Feb, 2021, 10:57: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by Yuvrajkumar92005 | 15 Oct, 2019, 08:24: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by Narendravignesh | 09 Oct, 2019, 06:02: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by arajeevshashank | 25 Sep, 2019, 12:26: PM
ANSWERED BY EXPERT
