Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 9 Answered

Prove that of all the parallelograms of the given sides, a rectangle has the greatest area.
Asked by Topperlearning User | 17 Aug, 2017, 12:23: PM
answered-by-expert Expert Answer
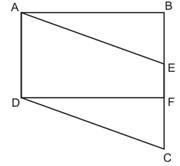
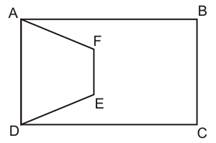
ABCD is a rectangle and ABFE is a parallelogram, such that
AD = BC = AE = BF
Area of rectangle = base x altitude
                             = AB x AD
Area of parallelogram ABFC = base x altitude
                                                = AB x EG
In AGE, AE > EG    (AE is the hypotenuse of right triangle)
But AD = AE
AD > EG
Hence, ar(rectangle ABCD) > ar (parallelogram ABFE)
Answered by | 17 Aug, 2017, 02:23: PM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 9 - Maths
Which of the following figures lie on the same base and between the same parallels? Write the common base and the two parallels.(I) (II)
Asked by Topperlearning User | 17 Aug, 2017, 12:27: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Prove that the area of a parallelogram is the product of any base of it and the corresponding altitude.
Asked by Topperlearning User | 17 Aug, 2017, 12:14: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
ABCD is a quadrilateral and BD is one of its diagonals as shown in the figure. DC= 5 cm, Altitude=10 cm. Show that ABCD is a parallelogram. Find its area.
Asked by Topperlearning User | 17 Aug, 2017, 12:18: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Show that line segment joining the mid points of a pair of opposite sides of a parallelogram, divides it into two equal parallelograms.
Asked by Topperlearning User | 17 Aug, 2017, 12:18: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
If E, F, G and H are respectively the mid points of the sides of a parallelogram ABCD, show that ar(EFGH) = ar(ABCD).
Asked by Topperlearning User | 17 Aug, 2017, 12:25: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
In the square ABCD of side 10 cm E and F are the mid points of AD and BC. Find the area of APE.
Asked by Topperlearning User | 17 Aug, 2017, 12:26: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
In a parallelogram PQRS, Take a point A on RS and join P and Q. In how many parts, the parallelogram is divided? What are the shapes of these Parts? Divide the parallelogram into two parts of equal area.
Asked by Topperlearning User | 17 Aug, 2017, 12:21: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
In a parallelogram ABCD, AB = 20 cm. The altitude corresponding to the side AB and AD are 14 cm and 10 cm respectively. Find AD.
Asked by Topperlearning User | 17 Aug, 2017, 12:22: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Prove that of all the parallelograms of the given sides, a rectangle has the greatest area.
Asked by Topperlearning User | 17 Aug, 2017, 12:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
If each diagonal of a quadrilateral separates it into two triangles of equal area, then show that the quadrilateral is a parallelogram.
Asked by Topperlearning User | 17 Aug, 2017, 12:24: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×