Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

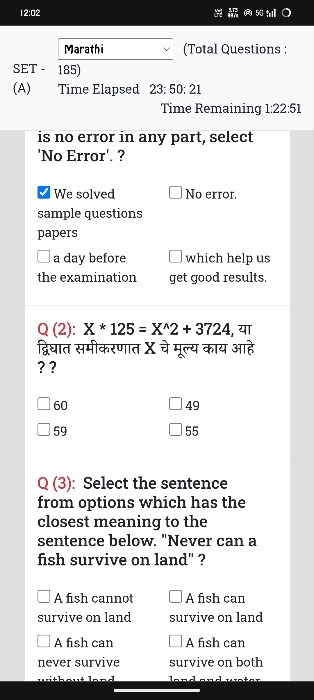
prove that 4 minus square root of 3 is an irrational number  
Asked by koushalvishal109 | 28 Feb, 2019, 02:16: PM
answered-by-expert Expert Answer
If 4-√3 is a rational number, then we can write  4-√3 = a/b  , where a and b are integers.
 
4-√3 = a/b
 
4 = ( a/b) +√3
 
4b = a + √3b
 
By squaring both sides, 16b2 = ( a +√3b )2 = a2 + 3b2 + 2√3ab
 
(13b2 - a2)/(2ab)  = p/q  = √3
 
where p = (13b2 - a2) and q = 2ab  are integers.
 
But right side of above equation is a irrartional number  that can not be equal to p/q if p and q are integers
 
we get this contradiction due to the assumption that 4-√3 is a rational number.
 
Hence 4-√3 is an irrational number
Answered by Thiyagarajan K | 28 Feb, 2019, 03:03: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
cos80÷ sin10+cos59• cosec31
Asked by raopaidi | 25 Apr, 2024, 04:06: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
2/x+2/3y=1/6; 3/x+2/y=0
Asked by aditikaldate7 | 21 Apr, 2024, 03:16: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
ABCD is a rectangle in which diagonal AC is equals to 17 cm angle BCA is equals to thitha and sin theta is equals to 8/17 find the area of rectangle ABCDE (ii) the perimeter of rectangle ABCD
Asked by pathaksuman622 | 21 Apr, 2024, 11:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
PQ is a chord of length 8 cm to a circle of radius 5 cm. The tangents P and Q intersect at a point T. Find the length of the tangent TP.
Asked by yalagondanikhil | 16 Apr, 2024, 12:25: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
if one of the zeroes of quadratic polynomial F(x) = 4x² - 8kx - 9 is equal in magnitude but opposite in sign, find K
Asked by rrajansinghakb199 | 08 Apr, 2024, 05:12: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
express 15.265 in p/q form?
Asked by nagalaxmidurgarao937 | 08 Apr, 2024, 01:42: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
the poles AB and CD of different heights are standing vertically on the ground level from a point P on the line joining the foots of the pole on the level of ground the angle of elevation to the top of the pole are founded to be complementary the of the CD and the distance PD 20√3m and 20m respectively if the BP is 10m then find the length of AB and the distance AC between the tpo of the poles
Asked by mraniruddha03 | 02 Apr, 2024, 06:44: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
from the pair of linear equations in the following problems and find their solution graphically 10 students of class 10 to part in a mathematic quiz if the number of girls is for more than the number of boys find the number of boys and girls who took part in the quiz
Asked by muttenenimalleswarrao | 29 Mar, 2024, 08:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
maths
question image
Asked by sonawnerohan01 | 23 Mar, 2024, 12:25: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
The distance of the point (5,-2) from x-axis will be :-
Asked by pathakvaishnavi9139 | 23 Mar, 2024, 10:45: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×