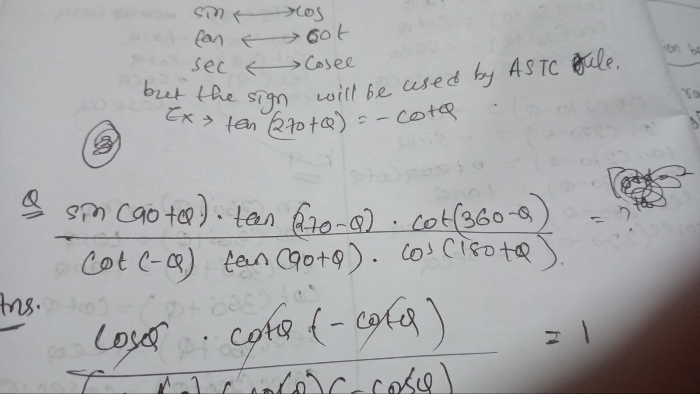CBSE Class 11-science Answered
Prove that cos2x cos(x/2)-cos3x cos(9x/2)=sin5x sin(5x/2)
Asked by Aarthi Vishwanathan | 01 Jun, 2012, 08:40: PM
Expert Answer
cos 2x cos(x/2) - cos 3x cos ( 9x/2 )
multiply and divide by 2, we get
1/2 [ 2 cos 2x cos ( x/2) - 2 cos 3x cos ( 9x/2 )]
using the formula ,
2 cos x cos y = cos(x+y) + cos(x-y) , we get ,
=1/2 [ cos ( 2x + x/2 ) - cos ( 2x - x/2 ) - cos ( 3x + 9x / 2 ) + cos ( 3x - 9x/2 )]
= 1/2 [ cos 5x/2 - cos 3x/2 - cos 15x/2 + cos3x/ 2]
= 1/2 [ cos 5x/2 - cos 15x/2]
= 1/2 [ -(- 2 sin 5x sin 5x/2 )]
= sin 5x sin 5x/2
Answered by | 01 Jun, 2012, 11:39: PM
Concept Videos
-
Trigonometric identities and problems
Fundamental trigonometric identities and problems based on them. Sign Conve... -
Degree measure and Radian measure ...
This video explains the concept of negative & positive angles, conversion o... -
Domain, period and range of trigonometric functions ...
Define the domain, period and range of the trigonometric functions and plot... -
Basic Trigonometric Formulae
Derive and apply the basic formulae of sine and cosine functions like sin(... -
Sign of Trigonometric Functions
This video covers values of trigonometric ratios of angles greater than 90 ...
CBSE 11-science - Maths
Asked by rajyothi64 | 05 Mar, 2024, 09:49: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by ghoshshawata62 | 04 Mar, 2024, 08:16: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by nayaktapaswini2007 | 29 Feb, 2024, 09:10: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by bimanmandal53361 | 15 Jan, 2024, 12:32: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by sreyas.katuri | 23 Sep, 2023, 07:12: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by 069.pks | 16 Sep, 2023, 10:06: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by surekhashriwas01 | 12 Sep, 2023, 08:39: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by mvr23467 | 12 Sep, 2023, 07:52: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by SasipriyaNagappan | 27 Jul, 2023, 07:22: PM
ANSWERED BY EXPERT
