Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

ICSE Class 10 Answered

Prove that both the roots of the equation (x-a)(x-b)=m^2 are always real.
Asked by Ananya | 18 Feb, 2018, 08:14: PM
answered-by-expert Expert Answer
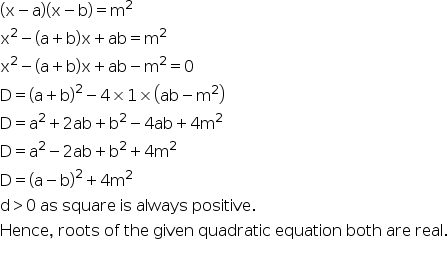
begin mathsize 16px style open parentheses straight x minus straight a close parentheses open parentheses straight x minus straight b close parentheses equals straight m squared straight x squared minus open parentheses straight a plus straight b close parentheses straight x plus ab equals straight m squared straight x squared minus open parentheses straight a plus straight b close parentheses straight x plus ab minus straight m squared equals 0 straight D equals open parentheses straight a plus straight b close parentheses squared minus 4 cross times 1 cross times open parentheses ab minus straight m squared close parentheses straight D equals straight a squared plus 2 ab plus straight b squared minus 4 ab plus 4 straight m squared straight D equals straight a squared minus 2 ab plus straight b squared plus 4 straight m squared straight D equals open parentheses straight a minus straight b close parentheses squared plus 4 straight m squared straight d greater than 0 space as space square space is space always space positive. Hence comma space roots space of space the space given space quadratic space equation space both space are space real. end style
Answered by Sneha shidid | 19 Feb, 2018, 10:01: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
ICSE 10 - Maths
When do we use nature of the roots formula in quadratic  equations word problem?-thanks
Asked by rashikulkarni28 | 18 Jul, 2022, 10:54: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
8x^2+(m+5)x + (m-1) =0
Asked by mohitmore008 | 30 Jun, 2022, 08:16: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
Find the value of discriminant of quadratic equation 2x² -3x -4 = 0
Asked by siddghode4371 | 28 Sep, 2021, 10:04: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
one root of the quadratic equation x^2-12x+a=0 is thrice the other. find the value of a
Asked by amit.clw4 | 22 May, 2021, 07:08: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
For what value of ‘k’ will the following quadratic equation: (𝑘 + 1)𝑥^2 − 4𝑘𝑥 + 9 = 0 have real and equal roots? Solve the equations.   please do the second part (solve the equations)
Asked by vineetachaturvedi11 | 04 Sep, 2020, 09:17: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
x²+2√3x _ 9 = 0
Asked by triptiagarwal910 | 09 Jun, 2020, 11:41: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
​​​​​​(4-k)x^2 + (2k+4)x + (8k+1) = 0 
Asked by saitipparthi79.10spicertl | 14 May, 2020, 09:20: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
factorise 7x^2-9x+2
Asked by thakurjyoti016 | 30 Mar, 2020, 12:10: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
For what value of k , (4-k)x2 +(2k+4)x +(8k+1) = 0 is a perfect square  
Asked by agupte28 | 27 Jul, 2019, 05:56: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
Find the value of k for which the roots of this equation are real and equal k^2 x^2 - 2(2k-1)x + 4= 0 
Asked by Ashutosh | 21 Feb, 2018, 07:51: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×