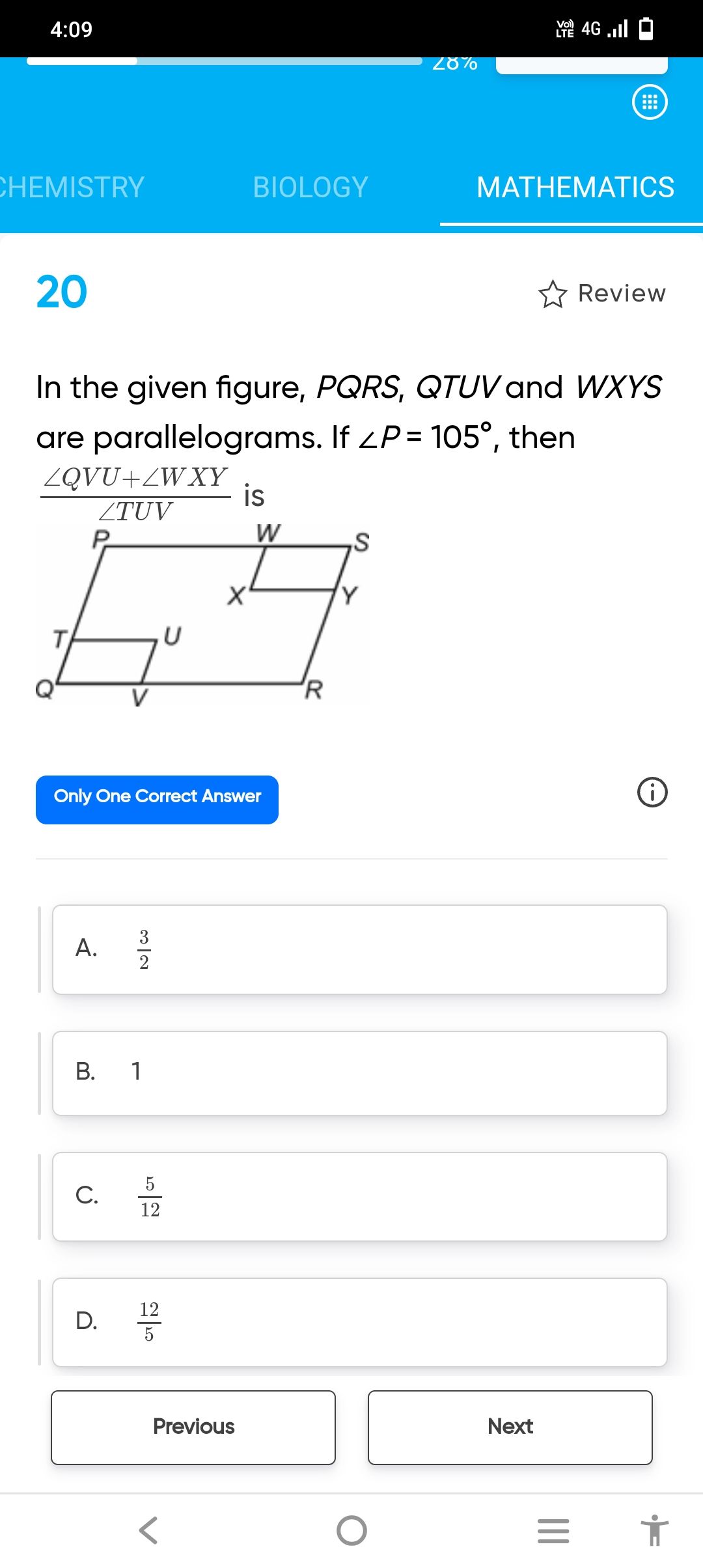
CBSE Class 9 Answered
prove that area of a rhombus is half the area of its diagonals
Asked by ayush kumar | 03 Mar, 2011, 01:54: AM
Dear Student,
Area of rhombus ABCD = area of triangle ABD + area of triangle CBD
Triangles ABD and CBD are congruent by SSS
Area of rhombus ABCD = 2×(Area of triangle ABD)
AE is perpendicular to DB because the diagonals of a rhombus are perpendicular bisectors of each other.
Area of triangle ABD = DB×AE/2 because a triangle's area is one-half the product of a side and the altitude drawn to that side.
Area of rhombus ABCD = 2×(Area of triangle ABD)
So area of rhombus ABCD = 2×(DB×AE/2) = DB×AE
AE = AC/2 because the diagonals of a rhombus are perpendicular bisectors of each other.
So area of rhombus DB×AE = DB×(AC/2) = DB×AC/2
Hence area of a rhombus is half the area of its diagonals
Regards
Team Topperlearning
Answered by | 02 Mar, 2011, 10:54: PM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by chandininayak86 | 15 Dec, 2023, 07:36: AM
CBSE 9 - Maths
Asked by sagrawal0081 | 31 Aug, 2023, 07:24: PM
CBSE 9 - Maths
Asked by jahnavinehra | 03 Jul, 2022, 11:19: AM
CBSE 9 - Maths
Asked by seemarana8535 | 11 May, 2022, 04:17: PM
CBSE 9 - Maths
Asked by abhiroy1462 | 16 Apr, 2022, 02:25: PM
CBSE 9 - Maths
Asked by abdullahzedane2008 | 28 Mar, 2022, 12:11: PM
CBSE 9 - Maths
Asked by sanskritiraghudev | 19 Feb, 2022, 09:38: AM
CBSE 9 - Maths
Asked by varundhawan | 31 Jan, 2022, 10:41: PM
CBSE 9 - Maths
Asked by aziznoorani17 | 04 Jan, 2022, 11:32: AM
CBSE 9 - Maths
Asked by vineetyadav77050 | 25 Jul, 2021, 05:45: PM