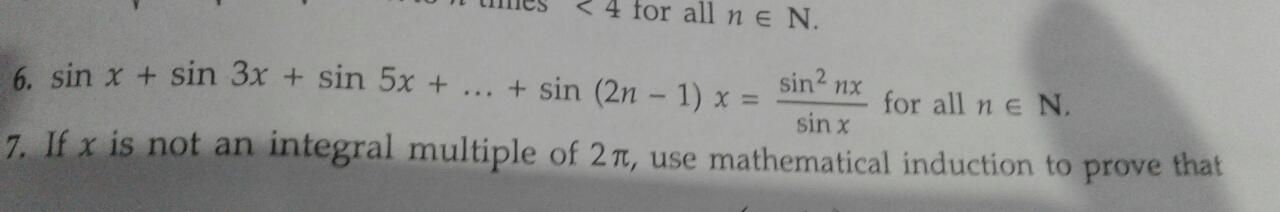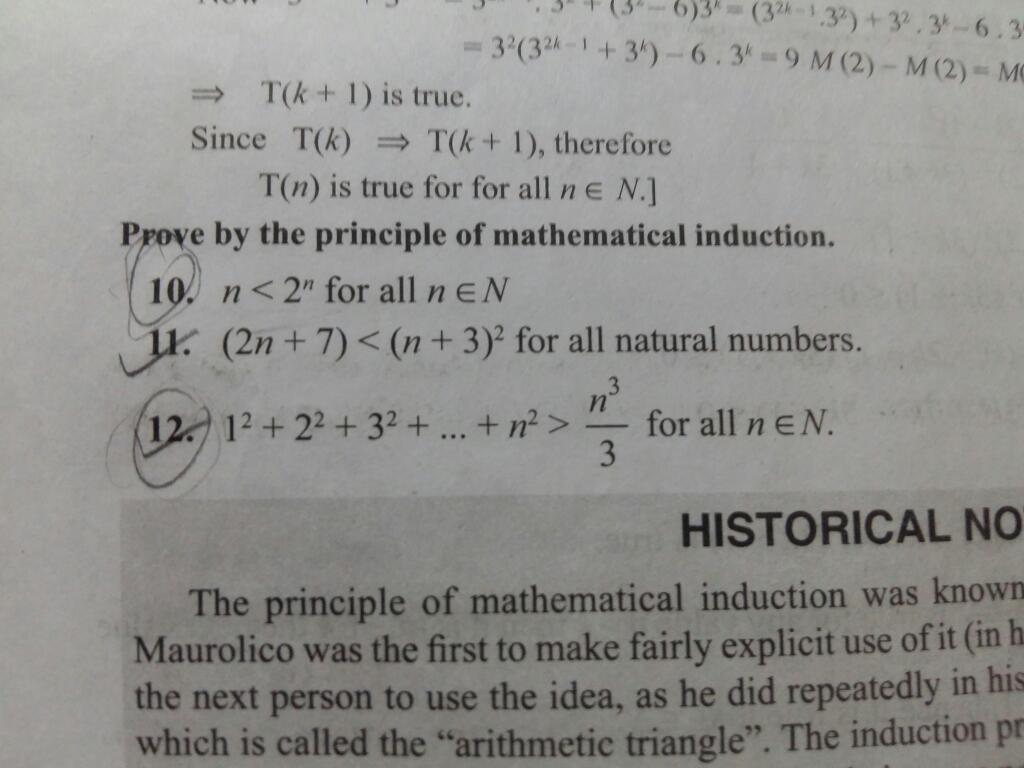CBSE Class 11-science Answered
Prove by using the principle of mathematical induction 32n – 1 is divisible by 8 for n 
N.
N.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
Expert Answer
Let P(n) : 32n – 1 is divisible by 8.
P(1): 32 – 1 = 8 which is divisible by 8. Thus P(n) is true for n = 1.
Let P(k) be true for some natural number k.
i.e. P(k): 32k – 1 is divisible by 8.
Let 32k – 1 = 8d, where d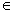 
N.
N.Now we prove that P(k + 1) is true whenever P(k) is true.
Now, 32(k + 1) – 1 = 32k.32 – 1
= (8d + 1).32 – 1
= 9.8d + 9 – 1
= 8(9d + 1)
32(k + 1) – 1 is divisible by 8. Thus P(k +1) is true whenever P(k) is true.By principle mathematical induction 32n – 1 is divisible by 8 for all n N.
Answered by | 04 Jun, 2014, 03:23: PM
Concept Videos
-
Application of Mathematical Induction
This video explains the Principle of Mathematical Induction to prove the va... -
Application of Mathematical Induction
This video explains the use of Principle of Mathematical Induction to prove... -
Problem solving on principles of mathematical induction ...
Use the Principle of Mathematical Induction to prove the validity of statem...
CBSE 11-science - Maths
Asked by syedaliasad649 | 01 Oct, 2019, 07:07: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by lovemaan5500 | 02 Feb, 2019, 08:24: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
N.Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by Topperlearning User | 15 May, 2014, 11:50: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
N.Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
If P(n) is the statement 72n + 23n - 3.3n - 1 is divisible by 25 for all n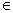 
N, then what is P(k + 1)?
N, then what is P(k + 1)?
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
N.Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT
