CBSE Class 11-science Answered
Let
f(n) = n7 - n
Let M(6) mean 'is a multiple of 6', and M(7)
mean 'is a multiple of 7'.
f(n) = n(n6 - 1)
= n(n3 - 1)(n3 + 1)
= n(n-1)(n2+n+1)(n+1)(n2-n+1)
= (n-1)n(n+1)(n2-n+1)(n2+n+1)
since we have factors (n-1)n(n+1) we have 3 consecutive numbers and
the product of ANY 3 consecutive numbers will be divisible by 2 and
also by 3, so therefore also by 6.
The problem reduces to showing that n7 - n = M(7). We will do that
by induction:
Show that it is true for a particular value of n, say n=2.
27 - 2 = 126 = 7 x 18 = M(7)
Assume it is true for some value n=k, so we assume:
f(k) = k7 - k = M(7)
Now consider the next value n=k+1
We must show that f(k+1) is also M(7)
f(k+1) = (k+1)7 - (k+1)
= k7 + 7C1k6 + ..... + 7C6k + 1 - (k+1)
= k7 - k + M(7) + 1 - 1
= k7 - k + M(7)
k7 - k is divisible by 7 and so the whole expression for f(k+1) is divisible by 7.
So if f(k) is M(7) then we have shown that f(k+1) is also M(7).
Whenever f(k) is divisible by 7
Therefore n7 - n is always divisible by both 6 and 7 and therefore
it is divisible by 42







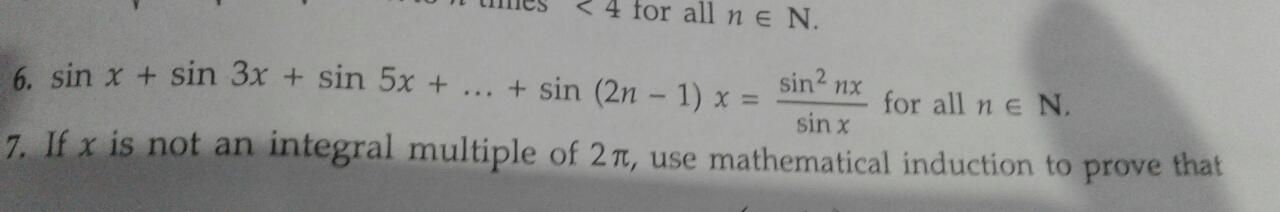
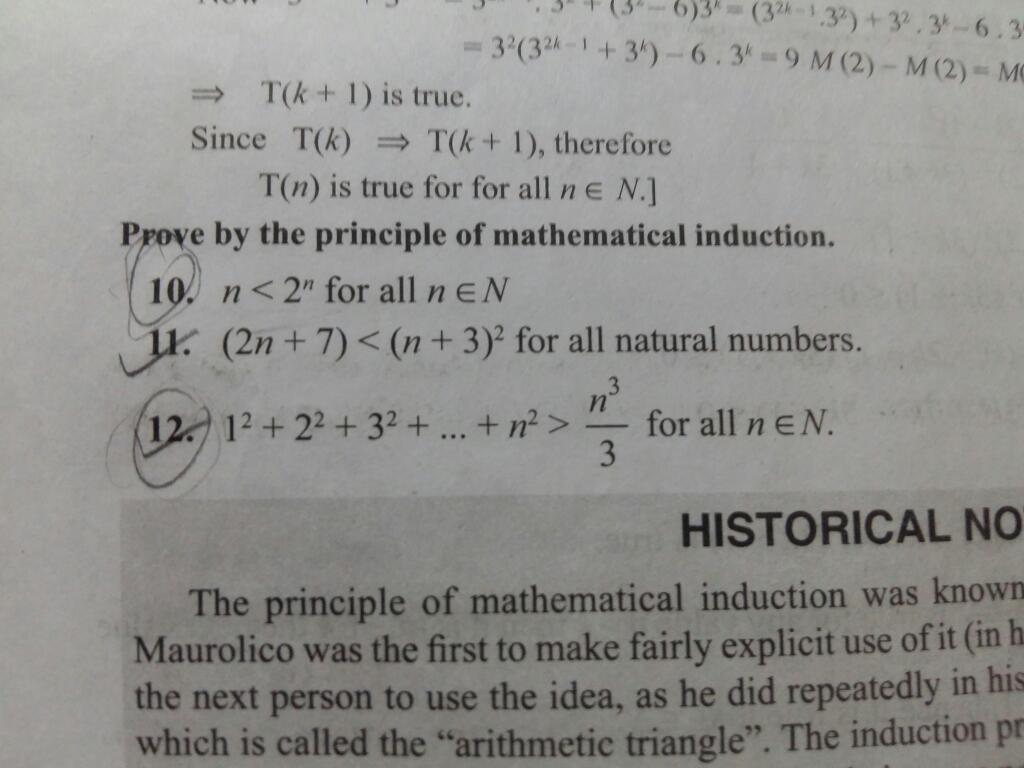
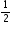 n(3n-1)
n(3n-1)