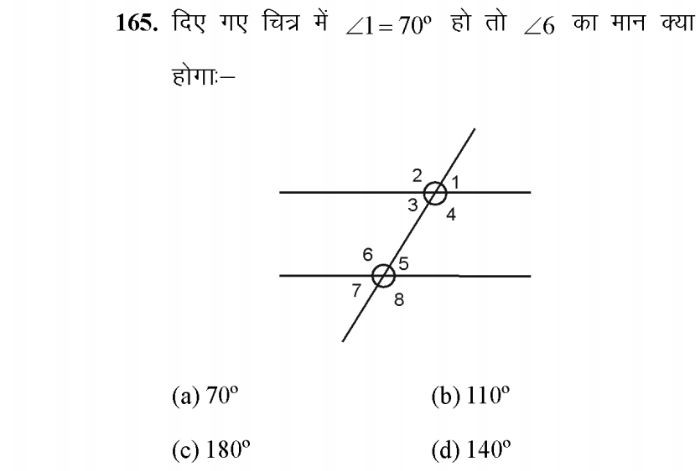
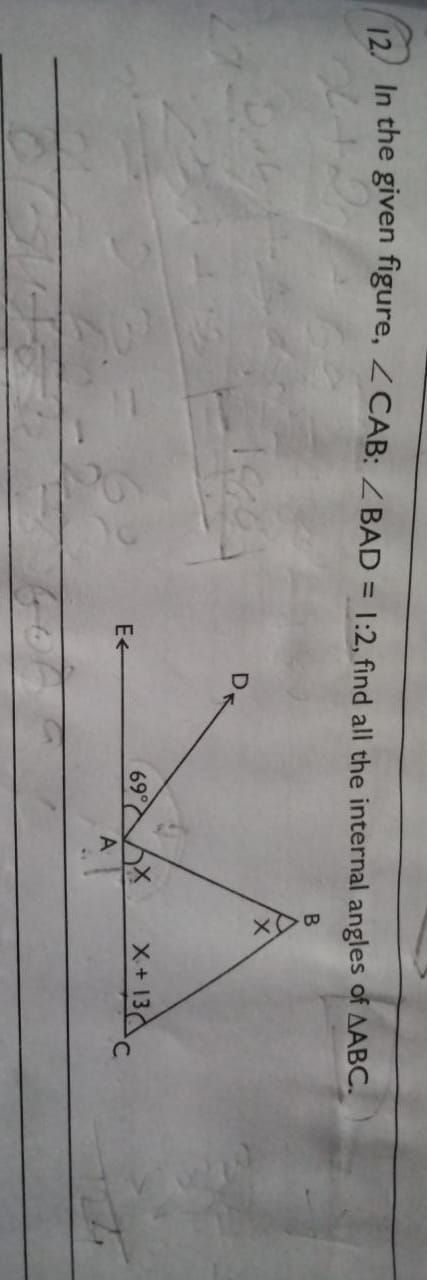
CBSE Class 9 Answered
proove that
Asked by | 14 Mar, 2009, 04:32: PM
Expert Answer
Let that the angle bisectors of the said angles meet at P and ACD be the exterior angle of the base angle C.
So,
in triangle PBC,
angle PBC=1/2(B)...(as BP is the bisector of angle ABC)
angle PCB
=PCA+ACB
=1/2(angleACD)+C
=1/2(180-C)+C
=90-(C/2)+C
=90+(C/2)
So using angle sum property for triangle BPC, we get,
P+PBC+PCB=180
So,
P+1/2(B)+90+(C/2)=180
So,
P+[(B+C)/2]=90
So,
P+[(180-A)/2]=90.. (as B+C=180-A)
So,
P+90-(A/2)=90
So,
P=A/2
Hence proved.
Answered by | 14 Mar, 2009, 06:31: PM
Application Videos
-
Co-Interior Angles - 2
This video explains the solution of the given problem which is based on Pro... -
Angle Sum Property of a Triangle - 1 ...
This video contains a question which is solved using the interior angle pro... -
Angle Sum Property of a Triangle - 2 ...
This video covers the interior angle property of a triangle with the help o... -
Angle Sum Property of a Triangle - 3 ...
This video explains how to find the measurement of an interior angle by usi... -
Comlpementary and Supplementary Angles ...
This video explains an application based problem on Comlpementary and Suppl...
Concept Videos
-
Basic Concepts of Geometry
This video explains the basic geometrical concepts like line and angle, var... -
Transversals, interior and exterior angles made by them ...
Transversals, interior and exterior angles made by them with a pair of para... -
Angle Sum Property of A Triangle
Find the sum of the interior angles of a triangle. Establish the relation ... -
Parallel Lines and Co-Interior Angles ...
Parallel Lines & Co-Interior Angles -
Basic geometrical concepts
Basic geometrical concepts like line and angle, various types of angles & t...
CBSE 9 - Maths
Asked by roshan.rony001 | 19 Sep, 2023, 05:02: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by pushpadevipushpadevi19 | 13 Jan, 2023, 08:06: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by savitamahajan202 | 02 Jan, 2023, 10:55: AM
ANSWERED BY EXPERT
CBSE 9 - Maths
Asked by amarjitruksh | 20 Jun, 2022, 10:40: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by Abhishita9 | 12 Nov, 2021, 06:41: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by raghavgargrg28 | 10 Sep, 2021, 05:11: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by kamateganpati | 08 Sep, 2021, 06:17: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by swatipuspapatel | 07 Feb, 2021, 07:29: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by saritaagarwal30121980 | 14 Oct, 2020, 10:07: AM
ANSWERED BY EXPERT
