CBSE Class 9 Answered

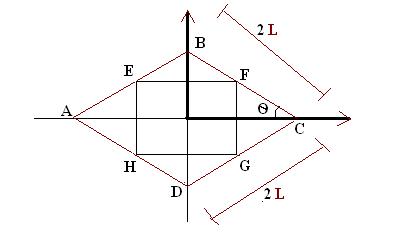
Let P be the point of intersectionof ED and FC.

ABCD is given to be a rhombus. This means that the diagonals AC and BD bisect each other at right angles.

So if O is the point of intersection of the diagonals, then AO=OC and DO=BO.

Consider triangle EBD.

given that EA=AB  and we also have BO=OD

So, by the converse of mid point theorem,

AO must be parallel to ED.

This implies that ,

AC must be parallel to EP.

Next,

in triangle AFC,

AB=BF and  AO=OC.

So, again using converse of mid point theorem,

 we get,

BO  is parallel to CF.

but angle BOC=90  degrees , as the diagonals of a rhombus bisect each other at 90 degrees.

So,angle OCF=90  degrees, too as they are interior angles on the same side of the transversal and so, must be supplementary.

We have already proved that AC is parallel to EP.

This implies that angle OCF=angle EPF.

So, angle EPF=90 degrees, as they are corresponding angles .

Thus, we get that ED and CF when produced meet at right angles.