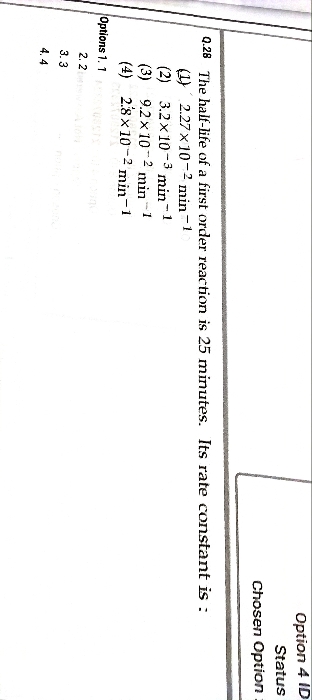
CBSE Class 12-science Answered
Pls solve this question.
Asked by suchananag2002 | 22 Mar, 2020, 10:10: AM
Expert Answer
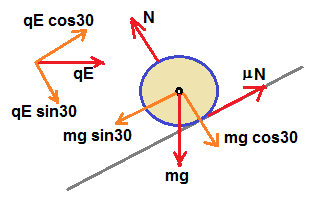
Forces acting on a charged ball that is slipping down on an inclined plane is shown in figure.
mg is weight, gravitational force that is resolved into two components.
One component mgsin30 which is parallel to inclined plane driving the ball down.
Other component mgcos30 acting perpendicular to surface of inclined plane.
qE is the electrostatic force, where q is charge of the ball and E is electric field.
This electrostatic force also is resolved into two components.
One component, qEcos30 is parallel to inclined plane surface that oppose the motion of the ball.
Other component qEsin30 which is perpendicular to the inclined plane surface.
Hence the normal reaction force = N = mgcos30 + qEsin30
Friction force μN = μ ( mgcos30 + qEsin30 )
Hence the net force driving the ball down = { mg sin30 - qE cos30 - μ ( mgcos30 + qEsin30 ) } ..............(1)
electro static force = qE = 0.01 × 100 = 1 N
Acceleration in the direction of ball's slipping motion = force / mass
using qE= 1 N and given value of friction coefficient μ = 0.2 ,
we get acceleration a from eqn.(1) as , a = 2.237 m/s2
Time taken t by the ball to slip down to bottom is obtained from " S = (1/2) a t2 "
where S is length of incline plane surface, i.e. 2 m
( height = 1m , angle 30o , hence length of inclined plane = 2 m )
= 1.337 s
Answered by Thiyagarajan K | 22 Mar, 2020, 05:40: PM
Concept Videos
-
Electric Charge - Part 1
This video describes the concept of charge, conductors and insulators, and ... -
Gold Leaf Electroscope - Part 1
This video explains the basic properties of electric charges. -
Coulom's Law of Electric Force - Part 1 ...
This video describes Coulomb's law to calculate the force between any two p... -
All about electric fields
Define electric field in terms of Coulomb's force. Apply superposition prin... -
Electric Field Lines
This video explains the representation of electric field due to a single ch...
CBSE 12-science - Physics
Asked by dasrituparna1999 | 13 Apr, 2024, 06:56: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by dasrituparna1999 | 12 Apr, 2024, 09:26: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by mishrigupta19319 | 08 Apr, 2024, 06:28: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by madhav9119887644 | 07 Apr, 2024, 08:10: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by mishrigupta19319 | 07 Apr, 2024, 11:23: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by adityagalar2007 | 06 Apr, 2024, 01:06: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by amlanmcob | 06 Apr, 2024, 12:27: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by hussain221man | 05 Apr, 2024, 08:44: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by mishrigupta19319 | 05 Apr, 2024, 12:01: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by manishamunda787 | 02 Apr, 2024, 11:07: AM
ANSWERED BY EXPERT
