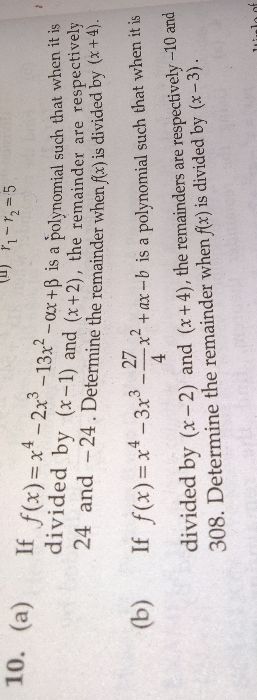CBSE Class 9 Answered
Pls help me with this question..
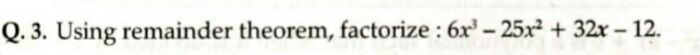
Asked by supriya3020kumari | 19 Jun, 2020, 08:44: PM
Expert Answer
We need to factorise the polynomial p(x) = 6x3 - 25x2 + 32x - 12 using Remainder theorem
x - a is a factor of p(x) when the remainder is zero by dividing p(x) by x - a
Take x = 1 i.e dividing by x - 1, so the remainder would be p(1)
p(1) = 6(1)3 - 25(1)2 + 32(1) - 12 = 6 - 25 + 32 - 12 = 38 - 37 = 1 not equal to 0
Take x = 2
p(2) = 6(2)3 - 25(2)2 + 32(2) - 12 = 48 - 100 + 64 - 12 = 112 - 112 = 0
The remainder is 0
Therefore, x - 2 is the factor of p(x)
By dividing p(x) by x - 2, the quotient will be 6x2 - 13x + 6
p(x) = (x - 2)(6x2 - 13x + 6)
= (x - 2)(6x2 - 9x - 4x + 6)
= (x - 2)[3x(2x - 3) - 2(2x - 3)]
= (x - 2)(2x - 3)(3x - 2)
Answered by Renu Varma | 22 Jun, 2020, 01:02: PM
Application Videos
-
Remainder Theorem
This video contains a question which is solved using Remainder theorem
Concept Videos
CBSE 9 - Maths
Asked by palakbajwa21 | 24 May, 2023, 07:41: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by 1987daljeetkaur | 22 May, 2023, 11:54: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by shivalaxmi0205 | 21 Feb, 2023, 07:26: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by anikk659 | 08 Jan, 2023, 03:41: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by yeshudarsh | 05 Jul, 2022, 06:38: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by meghapatel29121998 | 23 Jun, 2022, 10:08: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by Chaitanyamburande | 08 May, 2022, 11:43: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by abdulsamad82007 | 26 Jun, 2021, 02:24: PM
ANSWERED BY EXPERT
