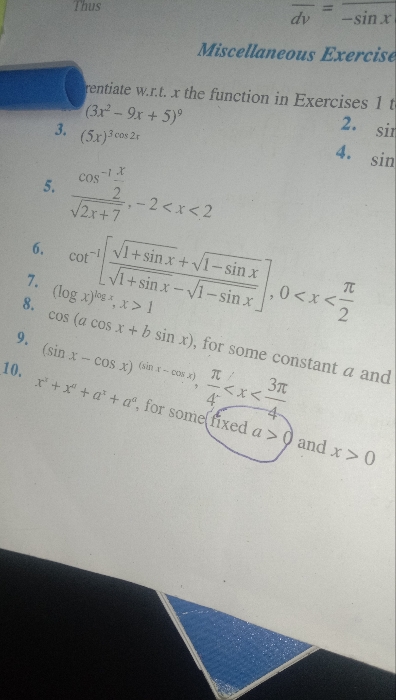CBSE Class 12-science Answered
please solve this.
Asked by prabhat1993 | 16 Feb, 2010, 07:50: PM
 |xsin(πx)| dx, limits, -1 to 3/2
|xsin(πx)| dx, limits, -1 to 3/2
From -1 to 0, x will be negative and sin function will also be negative. Hence their product will be positive.
It will also be positive from 0 to 1, it's only negative from 1 to 3/2.
Hence we can write,
 |xsin(πx)| dx, limits, -1 to 3/2 = I1 + I2 + (- I3 ) ............for the three limit parts mentioned above.
|xsin(πx)| dx, limits, -1 to 3/2 = I1 + I2 + (- I3 ) ............for the three limit parts mentioned above.
Now I1 = I2 =  x sin(πx) dx, with limits from 0 to 1
x sin(πx) dx, with limits from 0 to 1
= -xcos(πx) /π + sin(πx) /π2 ........integrating by parts,
Put the limits,
= 1/π
Similarly I3, limits,
I3 = -1/π2 + 1/π
Using these, we find,
 |xsin(πx)| dx, limits, -1 to 3/2 = 1/π + 1/π2 = (π + 1)/π2
|xsin(πx)| dx, limits, -1 to 3/2 = 1/π + 1/π2 = (π + 1)/π2
Regards,
Team,
TopperLearning.
Answered by | 17 Feb, 2010, 07:44: AM
Application Videos
Concept Videos
CBSE 12-science - Maths
Asked by aishaazmata | 24 Apr, 2024, 08:48: PM
CBSE 12-science - Maths
Asked by revengesena | 24 Apr, 2024, 06:08: PM
CBSE 12-science - Maths
Asked by mahammadsharifdakhani67 | 16 Apr, 2024, 07:43: PM
CBSE 12-science - Maths
Asked by 20muskaansharma23 | 08 Apr, 2024, 11:31: AM
CBSE 12-science - Maths
Asked by cherrycharishma512 | 01 Apr, 2024, 12:32: PM
CBSE 12-science - Maths
Asked by annapoornaa429 | 31 Mar, 2024, 08:23: PM
CBSE 12-science - Maths
Asked by shirishakuruva477 | 28 Mar, 2024, 09:52: PM
CBSE 12-science - Maths
Asked by sheensvlog | 27 Mar, 2024, 10:15: PM