CBSE Class 12-science Answered
Please solve and also explain the reason during the same...
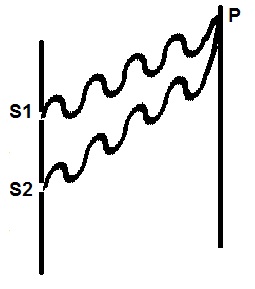
Let two waves from S1 and S2 interfere at P.
The two waves are given by
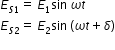
where δ is the phase difference between two waves
The resultant is given by
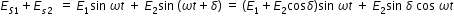
(student should workout the required trignometry/algebra here )
Above equation shows that superposition of two sinusoidal waves with same frequency but with
phase difference gives superposition of two sinusoidal waves of same frequency but different amplitudes.
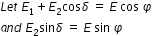
Where E is the resultant amplitude and φ is the resultant phase
By squaring and adding the above two equations we get
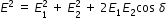
since Intensity I proportional to E2, we can write

If I1 = I2 = I0 and δ = 0, we get maximum Imax = 4I0
If I1 = I2 = I0 and δ = 2π, we get minimum Imin = 0
If I1 = I2 = I0 and δ ranging from 0 to 2π, we get intensity between Imax and Imin
which is given by I = (1+cosδ)2I0 .
When this intensity is averaged out for δ = 0 to 2π, we get average value 2I0
Hence the option (A) in the question is correct answer
Answered by | 04 Dec, 2017, 12:18: PM
Concept Videos
CBSE 12-science - Physics
Asked by shivamtkr7767 | 03 Mar, 2024, 12:45: PM
CBSE 12-science - Physics
Asked by tannusharan31 | 05 Nov, 2023, 05:31: PM
CBSE 12-science - Physics
Asked by mrwballari999 | 03 Jan, 2023, 09:33: AM
CBSE 12-science - Physics
Asked by neetaspirantdoctor | 20 May, 2022, 03:57: PM
CBSE 12-science - Physics
Asked by aryanshahi903 | 09 Apr, 2021, 06:14: AM
CBSE 12-science - Physics
Asked by nehadevi2728 | 19 Mar, 2021, 03:56: PM
CBSE 12-science - Physics
Asked by deepsmooth41 | 19 Apr, 2020, 01:00: AM
CBSE 12-science - Physics
Asked by ritikabehera01 | 20 Feb, 2019, 09:56: AM
CBSE 12-science - Physics
Asked by jain.pradeep | 18 Feb, 2019, 11:27: PM
CBSE 12-science - Physics
Asked by jain.pradeep | 18 Feb, 2019, 11:03: PM




 but where does the formula
but where does the formula  come from??
come from??


