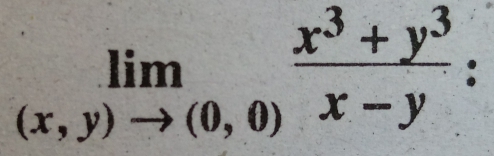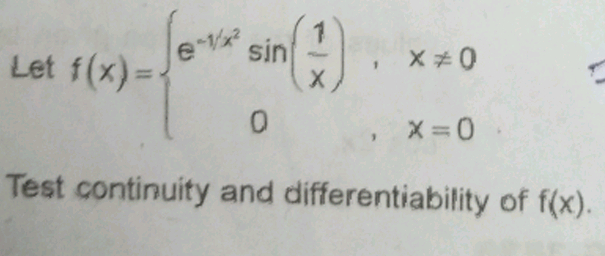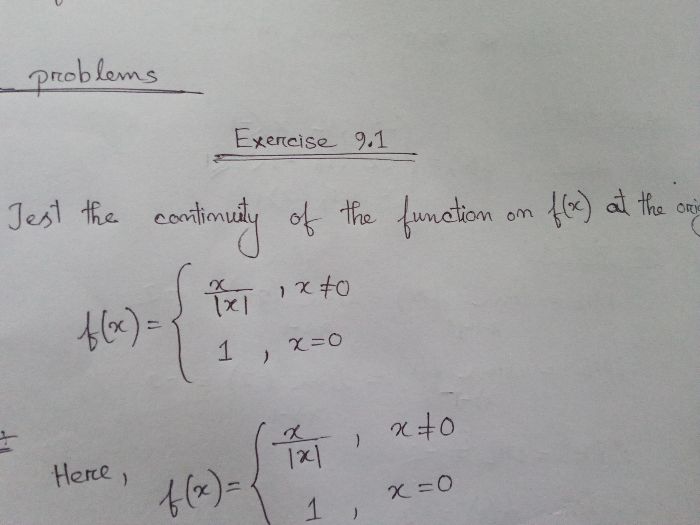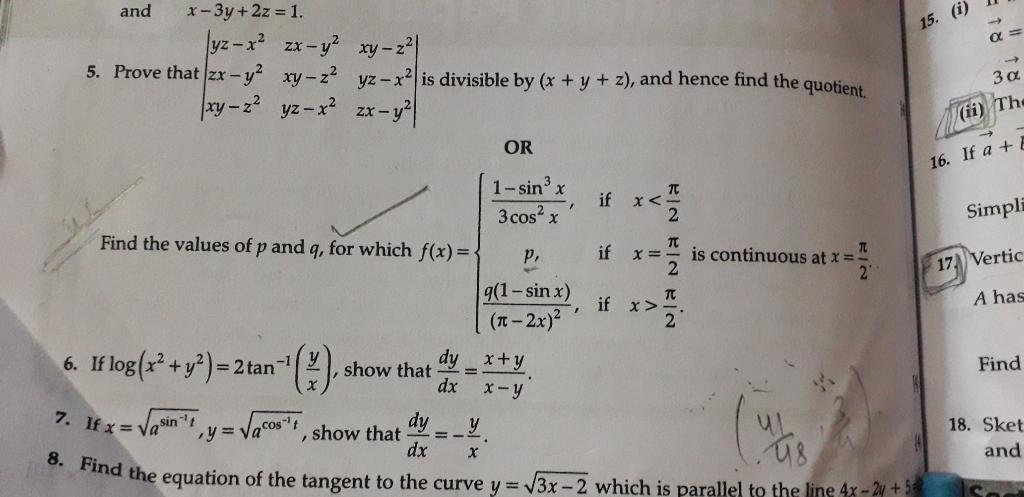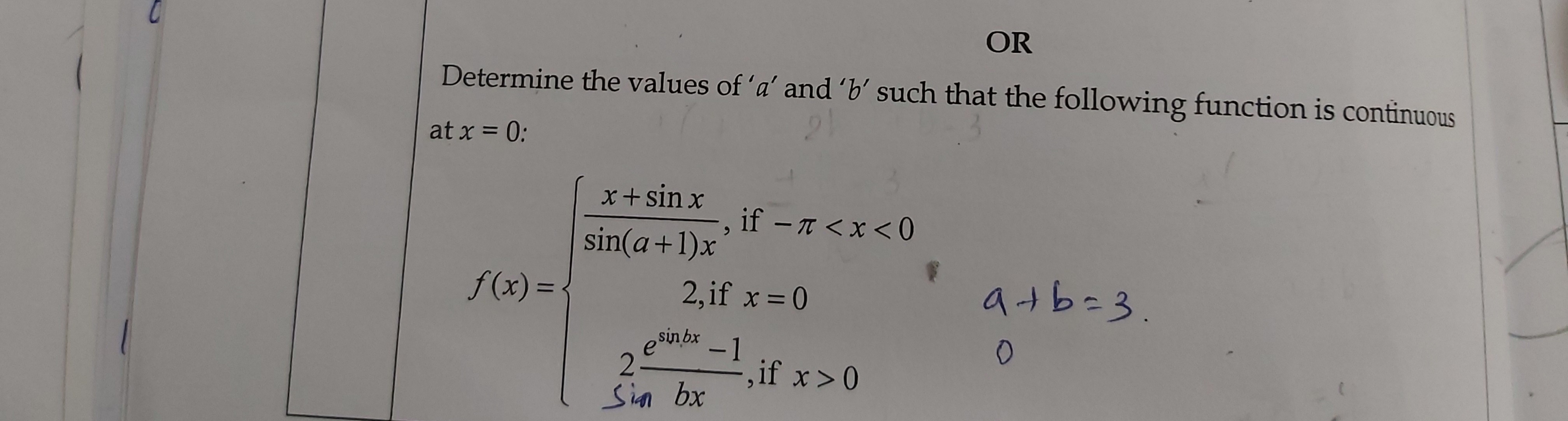CBSE Class 12-science Answered
Please help to find k given in the problem

Answered by Vijaykumar Wani | 04 Jul, 2016, 10:50: AM
Concept Videos
CBSE 12-science - Maths
Asked by fehasaf670 | 27 Jan, 2024, 01:39: PM
CBSE 12-science - Maths
Asked by sonkarmukesh007 | 13 Aug, 2023, 08:32: PM
CBSE 12-science - Maths
Asked by gurujellyar | 10 Sep, 2020, 08:13: PM
CBSE 12-science - Maths
Asked by jayshreechoudhury | 17 Aug, 2020, 11:22: AM
CBSE 12-science - Maths
Asked by rahmanafeef | 07 Apr, 2020, 11:32: PM
CBSE 12-science - Maths
Asked by lovemaan5500 | 07 Feb, 2020, 09:51: AM
CBSE 12-science - Maths
Asked by Shaikhshikha25 | 15 Oct, 2019, 12:09: PM
CBSE 12-science - Maths
Asked by saurabh91singh | 28 Sep, 2019, 11:38: AM
CBSE 12-science - Maths
Asked by jain.pradeep | 26 Sep, 2019, 11:18: PM
CBSE 12-science - Maths
Asked by musanjali.amd | 03 Sep, 2019, 11:57: PM