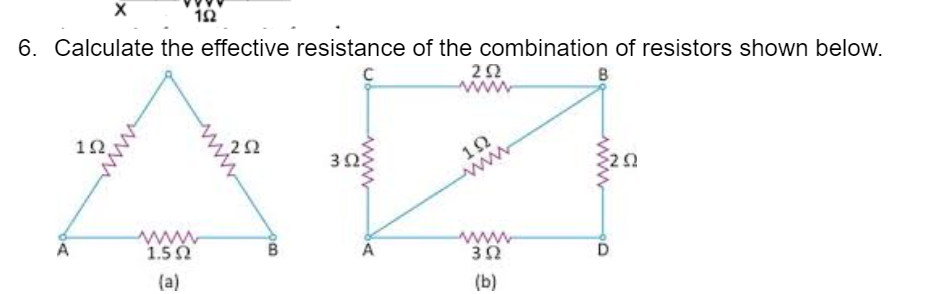
CBSE Class 10 Answered
please give me the explanation of this statement "the equivalent resistance is greater than the greatest resistance in the series combination "
as well as "the equivalent resistance is lesser than the least of all resistance in parallel combination"
pls explain me clearly
Asked by my3shyll | 28 Apr, 2016, 09:54: PM
In case of resistors connected in series the resultant resistance of a series combination (equivalent resistance) is the sum of individual resistances.
So, if there are 3 resistors say R1, R2 and R3 connected in series then the equivalent resistance (Rs) is given as
Rs = R1 + R2 + R3
Thus, we can see that the equivalent resistance is greater than all the resistances, ie., the value of equivalent resistor is greater than the resistor with the greatest value in the series combination.
i.e. Rs > R1 or R2 or R3
In case of parallel combination, the reciprocal of resultant resistance of a parallel combination of resistors (equivalent resistor) is the sum of reciprocals of individual resistances.
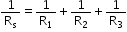
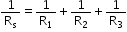
Thus, we can see that the equivalent resistance is lesser than all the resistances, ie., the value of equivalent resistor is lesser than the resistor with the greatest value in the series combination.
i.e. Rp < R1 or R2 or R3
Answered by Yashvanti Jain | 29 Apr, 2016, 07:38: PM
Application Videos
Concept Videos
CBSE 10 - Physics
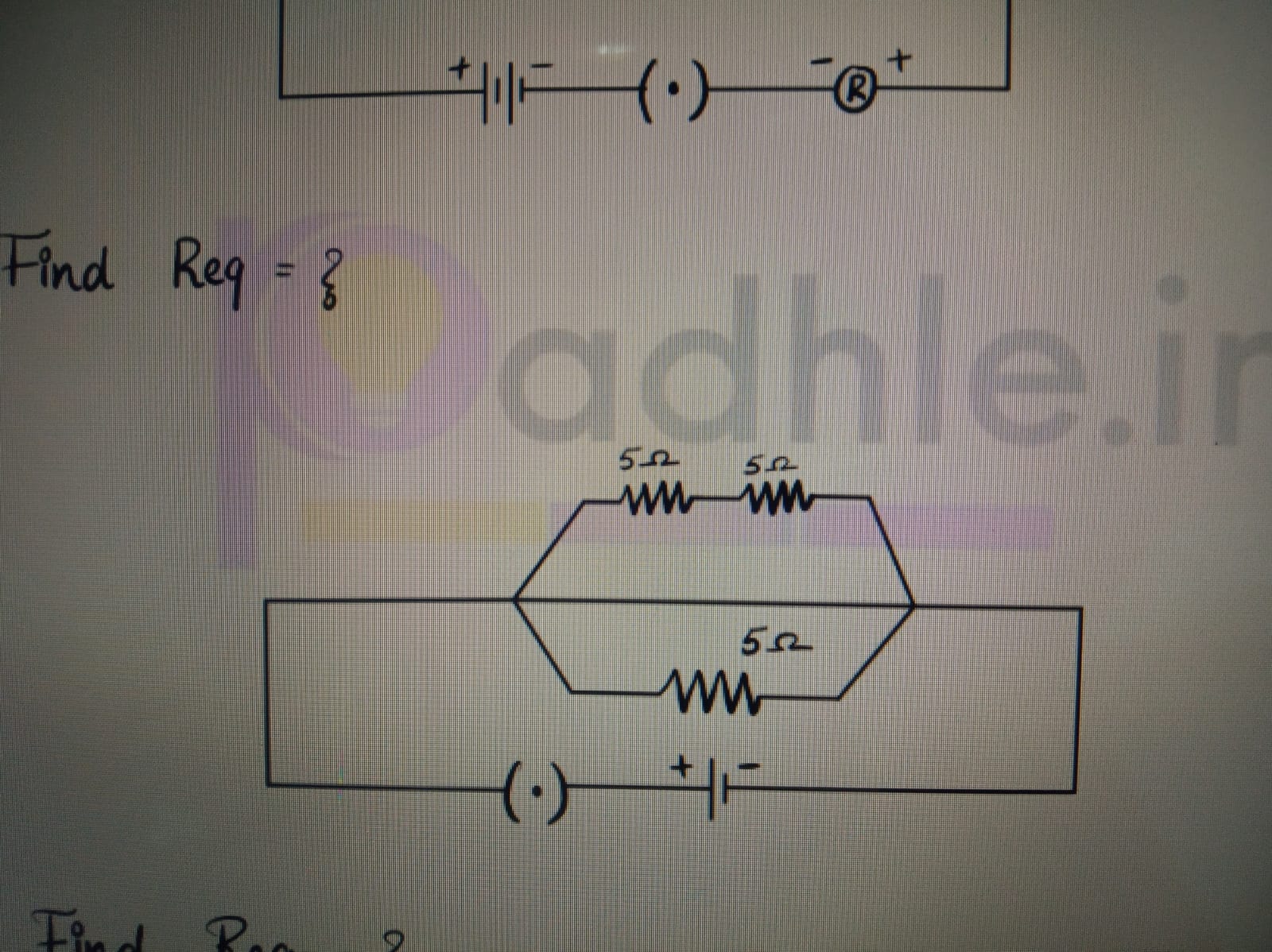
Asked by kamalaranjanmohantymohanty5 | 06 Jan, 2024, 10:05: AM
CBSE 10 - Physics
Asked by nandhikasugumar | 05 Oct, 2023, 04:01: PM
CBSE 10 - Physics
Asked by daniya062008 | 02 Oct, 2023, 08:25: PM
CBSE 10 - Physics
Asked by prassanna.j | 03 Sep, 2023, 12:28: PM
CBSE 10 - Physics
Asked by prassanna.j | 03 Sep, 2023, 12:21: PM
CBSE 10 - Physics
Asked by prassanna.j | 03 Sep, 2023, 12:11: PM
CBSE 10 - Physics
Asked by prassanna.j | 28 Aug, 2023, 09:49: PM
CBSE 10 - Physics
Asked by praveenkumae975 | 06 Feb, 2023, 07:19: PM