CBSE Class 12-science Answered

The diagram below on the left depicts two sources labeled S₁ and S₂ and separated by some distance d. Point P is a point on the screen that happens to be located on some nodal or antinodal line; as such, there is an order value (m) associated with this point. Point C is the central point on the screen. The distance from point P to point C as measured perpendicular to the central antinodal line will be referred to as y. The screen is located a distance of L from the sources. In the following derivation, the wavelength of light will be related to the quantities d, m, y and L.

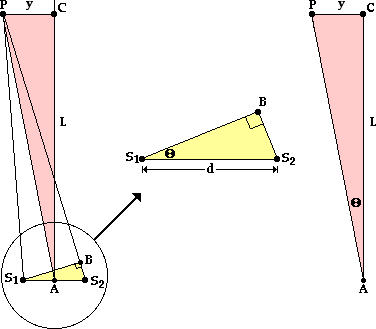
On the diagram above, source S₂ is further from point P than source S₁ is. The extra distance traveled by waves from S₂ can be determined if a line is drawn from S₁ perpendicular to the line segment S₂P. This line is drawn in the diagram on the left above; it intersects line segment S₂P at point B. If point P (a bright spot on the screen) is located a great distance from the sources, then it follows that the line segment S₁P is the same distance as BP. As such, the line segment S₂B is simply the path difference. That is, the small distance S₂B is equal to the difference in distance traveled by the two waves from their individual sources to point P on the screen. The logic is as follows:

	Assertion	Logic/Rationale
i	S2P = S2B + BP	See diagram above left
ii	PS1B =  PBS1	If screen is very far away (L >>> y), then lines S1P and BP are ||
iii	S1P = BP	If S1P and BP are || and line S1B is perpendicular to BP, then the length BP = length S1P
iv	S2P = S2B + S1P	Since S1P = BP, the expression S1P can be substituted into i
v	S2B = S2P - S1P	Algebraic manipulation of iv; subtract S1P from each side
vi	S2B is the PD	The path difference (PD) is defined as | S2P - S1P |

The yellow triangle in the diagram on the left above is enlarged and redrawn in the middle of the graphic. The triangle is a right triangle with an angle theta and a hypotenuse of d. Using the sine function, it can be stated that

But since it has been previously stated that the path difference (PD) is equal to the length of the line segment  S₂B, the above equation can be rewritten as

It can be further asserted that the pink triangle ( S₁BS₂) and the yellow triangle ( ACP) in the diagrams above are similar triangles. To prove that any two triangles are similar, one must show that they have two corresponding angles that are equal. Since the line segment PC was drawn perpendicular to the central antinodal line, it forms a 90-degree angle with the line AC. Thus, the corresponding angles S₁BS₂ and ACP are equal.

The second set of corresponding angles of equal measure is  S₁S₂B and  APC. This can be proven by returning to the assumption that the screen is very far away (L >>> y). Clearly, the lines S₁S₂ and PC are parallel lines. As such, the diagonal line S₂P creates two alternating angles that are equal in measure - that is, S₂PC = S₁S₂B. Since it is assumed that L >>> y, the line segment S₂P and AP are roughly parallel to each other and thus make roughly the same angle with the line segment S₁S₂. With this assumption, it is thus proven that  APC =  S₂PC. Since the  S₂PC is equal to both  S₁S₂B and  APC, it follows that  S₁S₂B =  APC. As such, the pink triangle (S₁BS₂) and the yellow triangle (ACP) have two corresponding angles that are equal and thus are similar triangles.

If the pink triangle (S₁BS₂) and the yellow triangle (ACP) are similar, all corresponding angles are equal in measure, and so S₂S₁B = PAC. These two angles are labeled as theta in the diagrams above. The use of trigonometric functions allows one to relate the angle theta to the reliably measured distances d, y and L.

sine  = PD / d

tangent  = y / L

The above logic has consistently assumed that the screen upon which the interference pattern is projected is very far away; that is, L >>> y. This is typically the case for visible light interference patterns. In fact, the L value is typically on the order of several meters while the y value is on the order of a couple of centimeters. For such dimensions, the angle theta is less than 1 degree. For such small angles, the approximation that the sine  = tangent  can be made. Taking 1 degree as a sample angle, calculated values of the sine and tangent can be compared.

Note that the values for the sine and the tangent of 1 degree show agreement out to the fourth significant digit. Since the sine and the tangent of these small angles are approximately equal, we can state that their ratio of lengths (as stated above) is also equal. That is,

In the previous section of Lesson 3, it was shown that the path difference (PD) for any point on the pattern is equal to m • , where m is the order number of that point and  is the wavelength. By substitution,

As a final step in the derivation, the equation can be algebraically manipulated so that the wavelength () is by itself:

 = y • d / (m • L)