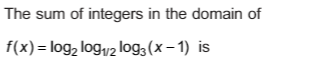CBSE Class 11-science Answered
Please explain:
Asked by nitishkrnehu09 | 01 Jan, 2018, 04:09: AM
following is the graph of [sinx]
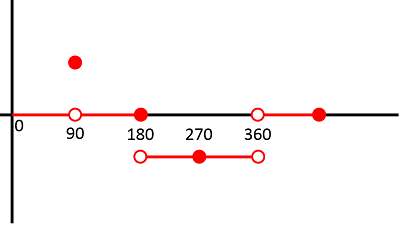
So continuous at 270o
Answered by Arun | 03 Jan, 2018, 05:56: PM
Concept Videos
CBSE 11-science - Maths
Asked by suryansh141107 | 16 Oct, 2023, 09:29: PM
CBSE 11-science - Maths
Asked by sohammukherjee0007 | 04 Oct, 2023, 11:01: AM
CBSE 11-science - Maths
Asked by sundramsingh1707 | 11 Jun, 2022, 05:20: PM
CBSE 11-science - Maths
Asked by maarcusfelix2006 | 24 Jul, 2021, 07:39: AM
CBSE 11-science - Maths
Asked by Jagannadhameshwar5 | 15 Jul, 2021, 09:17: PM
CBSE 11-science - Maths
Asked by seeni2005 | 12 Oct, 2020, 08:50: PM
CBSE 11-science - Maths
Asked by jasi01f4 | 06 Oct, 2020, 11:02: PM
CBSE 11-science - Maths
Asked by seeni2005 | 21 Sep, 2020, 03:04: PM
CBSE 11-science - Maths
Asked by rajvirsinhzala16 | 14 Aug, 2020, 12:43: PM
CBSE 11-science - Maths
Asked by hrishityelchuri2017 | 19 May, 2020, 09:58: AM