CBSE Class 11-science Answered
Please answer!!!!!! 


Asked by kpbhake | 24 Nov, 2017, 06:50: PM
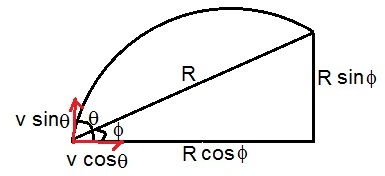
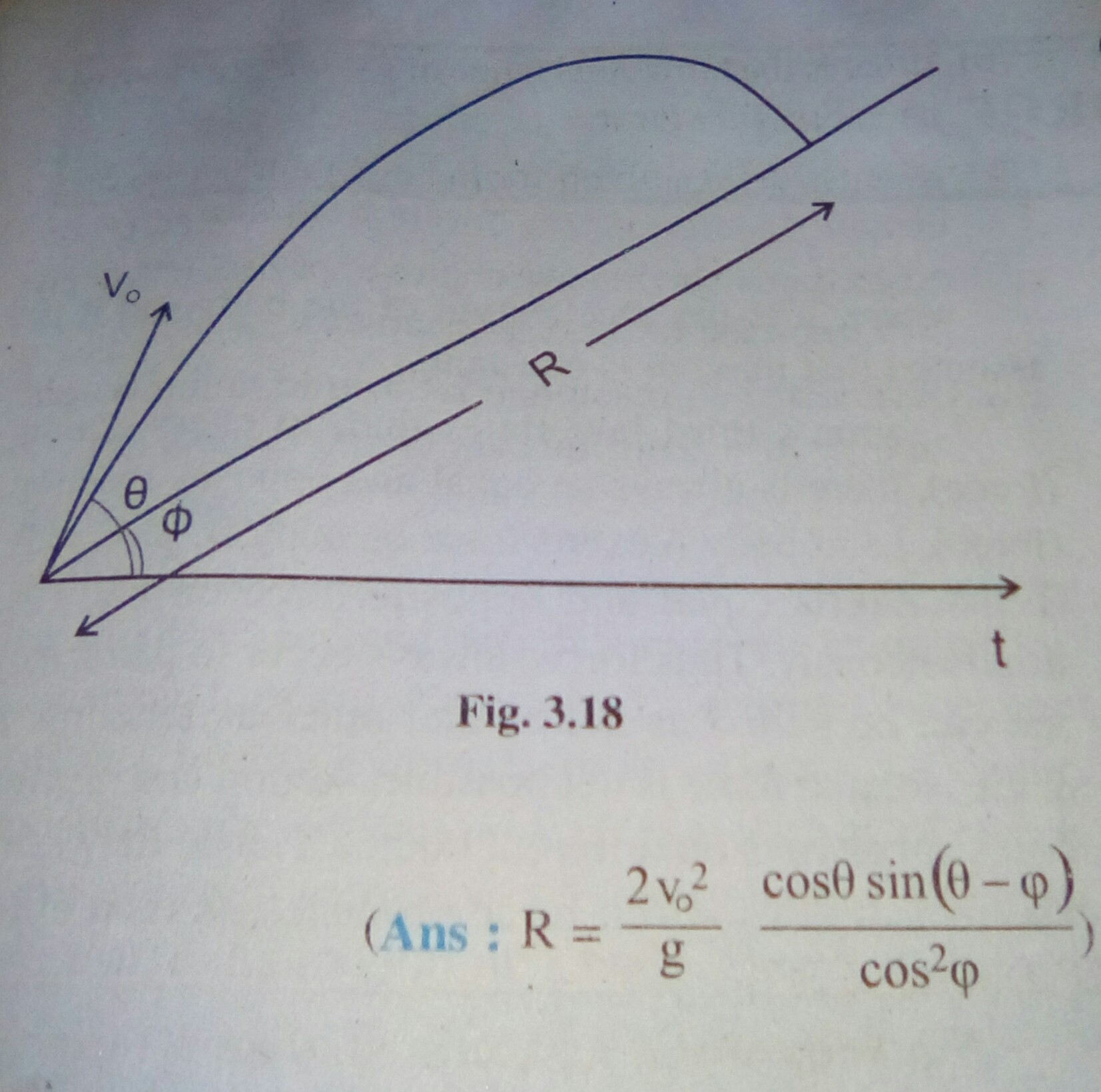
As per the figure, if R is the range in inclined plane, then horizontal distance travelled is Rcosφ and vertical distance travelled is Rsinφ.
time taken t for travelling Rcosφ is 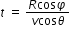
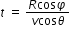
using the equation for t, we can write for vertical distance
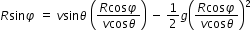
Cancelling out the common R throught all the terms and multiplying all the terms by 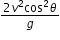 we get
we get
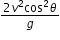 we get
we get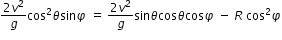
By rearranging the terms
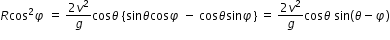
Hence
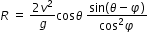
Answered by | 27 Nov, 2017, 02:48: PM
Concept Videos
CBSE 11-science - Physics
Asked by subhashreeojha235 | 16 Jul, 2023, 07:37: PM
CBSE 11-science - Physics
Asked by sush75 | 15 Mar, 2022, 04:02: PM
CBSE 11-science - Physics
Asked by abhishekchoudhary236 | 11 Nov, 2020, 10:09: PM
CBSE 11-science - Physics
Asked by chera5cibi | 28 Oct, 2020, 05:45: AM
CBSE 11-science - Physics
Asked by pushkarnannu4 | 05 Oct, 2020, 07:17: AM
CBSE 11-science - Physics
Asked by frontech990 | 06 Feb, 2019, 02:21: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Physics
The graph represents the velocity time for the first 4 seconds of motion. Find the distance covered. 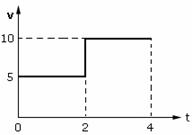

Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM