CBSE Class 9 Answered

Dear Student

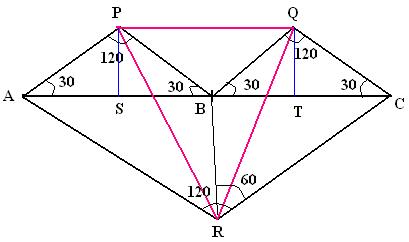
In the figure  PS, QT, RB  perpendicular bisectes the linesegments  AB, BC ,AC respectively

and AS=SB=BT=TC    and say it is equals to  r

AS=SB=BT=TC=r     ==>  (1)

Here I am going to prove that  BP=BQ=BR   and PBQ=QBR=RBP=120⁰

PBQ  =  180-30-30  =  120    ==>(1)

RBQ=90+30= 120                  ==>(2)

PBR=90+30= 120                  ==>(3)

Consider  PSD

PB Cos 30= SB  ==>   PB=  SB/cos30 =r/ ( 3  /2) = 2r /  3   ==>(4)

Similarly   QB =2r/3                                                                      ==>(5)

First let us find RC and then BR

Consider RBC 

RC cos30=BC=2r   ==>   RC= 2r/ (3/2)  =4r/3  

BR=RC cos 60 =  (4r/3) X  (1/2) =  2r/3            ==> (6)

Here I am going to prove that  BP=BQ=BR=2r/3   and PBQ=QBR=RBP=120⁰

This is a property of equilateral triangle

SO   PQR is an equilateral Triangle

Regards 

Team

Topper learning