CBSE Class 12-science Answered
Pl ans as fast as possible
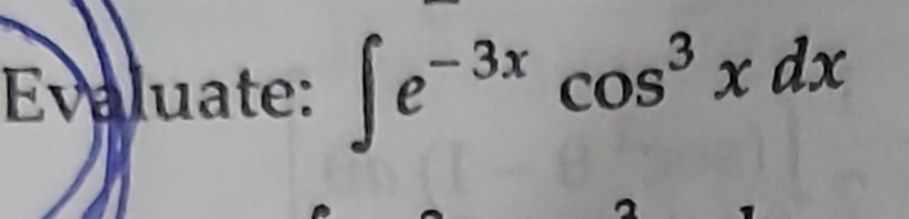
Asked by jain.pradeep | 10 Jan, 2020, 10:21: AM
To find the integration of e-3x cos3x
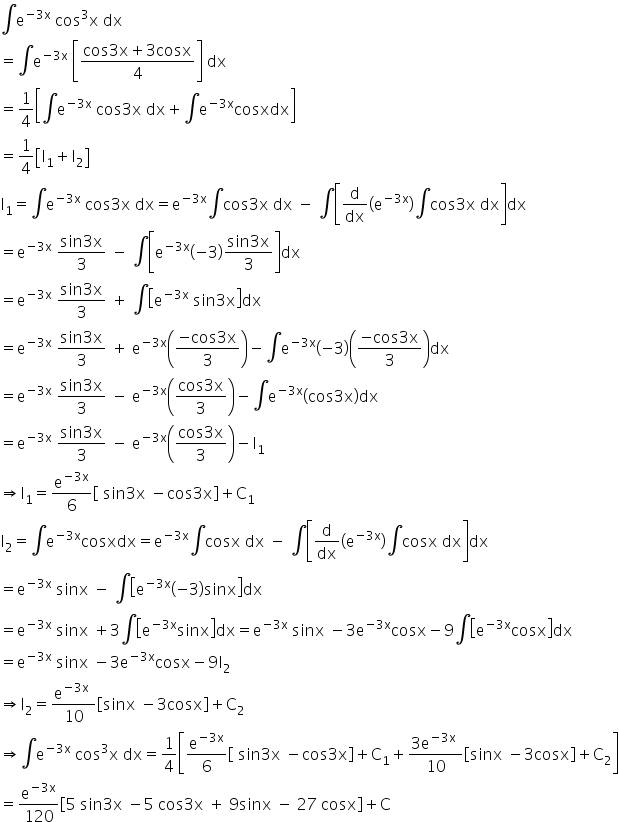
Answered by Renu Varma | 10 Jan, 2020, 11:50: AM
Concept Videos
CBSE 12-science - Maths
Asked by manyarajawat1 | 06 Nov, 2023, 05:03: PM
CBSE 12-science - Maths
Asked by dattashibani456 | 06 Apr, 2022, 01:07: PM
CBSE 12-science - Maths
Asked by sujachris1969 | 08 Jul, 2020, 04:47: PM
CBSE 12-science - Maths
Asked by jain.pradeep | 10 Jan, 2020, 10:21: AM
CBSE 12-science - Maths
Asked by Harsh | 25 Jul, 2019, 07:02: AM
CBSE 12-science - Maths
Asked by haroonrashidgkp | 29 Oct, 2018, 12:05: PM
CBSE 12-science - Maths
Asked by haroonrashidgkp | 28 Oct, 2018, 01:19: PM
CBSE 12-science - Maths
Asked by haroonrashidgkp | 18 Oct, 2018, 04:31: PM
CBSE 12-science - Maths
Asked by haroonrashidgkp | 18 Oct, 2018, 04:30: PM
CBSE 12-science - Maths
Asked by haroonrashidgkp | 18 Oct, 2018, 04:30: PM






