CBSE Class 10 Answered
Resistors in Series and in Parallel
When resistors, can be connected in such a way that the same current flows in them, then they are said to be connected in series. The resistors are said to be connected in parallel if the potential difference is the same across each resistor.
For any combination of resistors in a circuit, we can always find a single resistor that can replace the combination and result in the same total current and potential difference.
For example, a string of light bulbs can be replaced by a single, chosen light bulb that can draw the same current and have the same potential difference between its terminals as the original string of bulbs. The resistance of this single resistor is called the equivalent resistance of the combination.
- Resistances in Series
- Resistance in Parallel
Resistances in Series
If the resistances are connected end-to-end, the same current flows through each resistance, as there is no alternative path. Then

Now,
V = V1+V2+V3IRS = I1R1 + IR2 + IR3 Therefore,
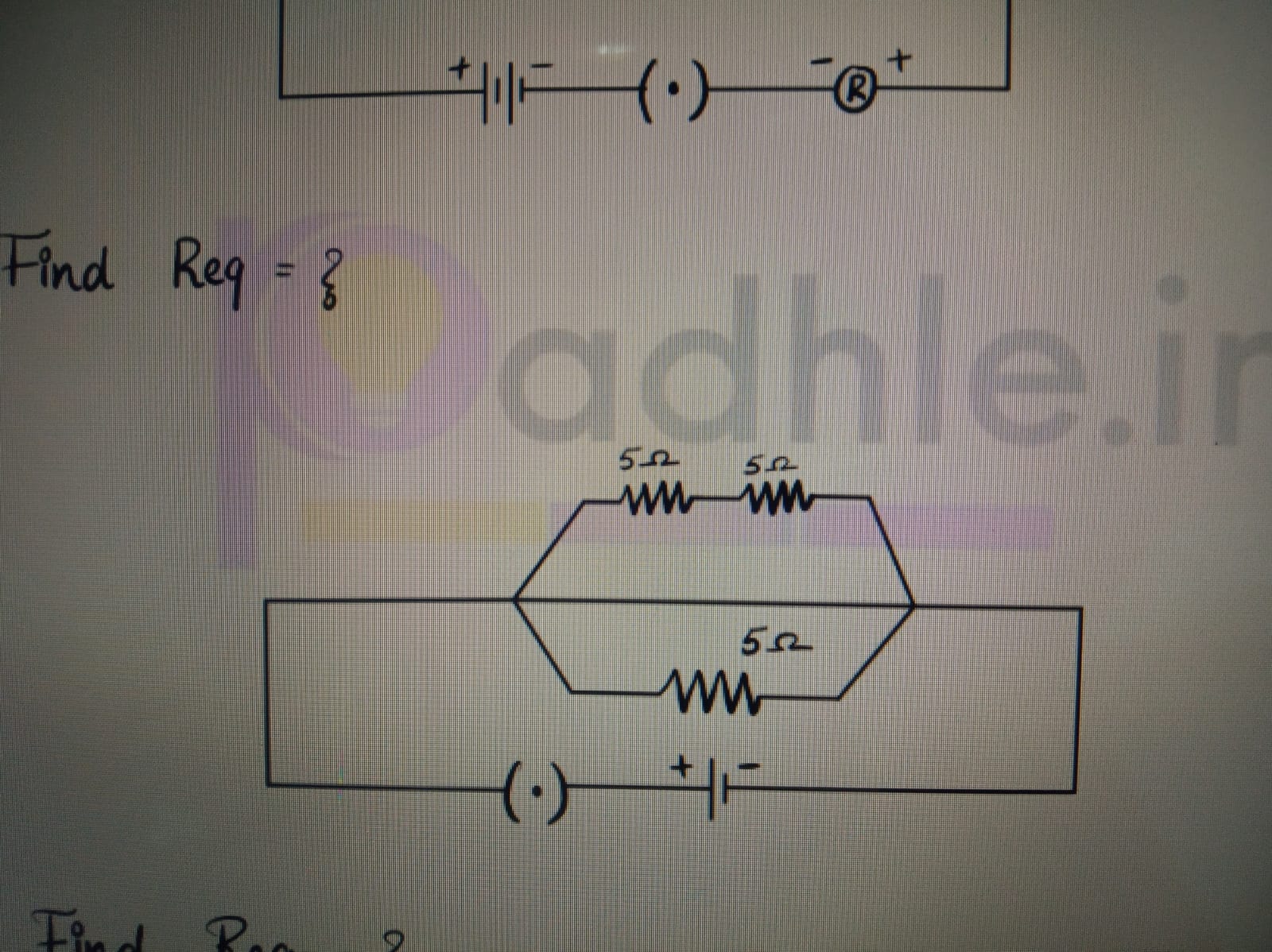
RS = R1+ R2 + R3Resistance in Parallel
If the resistance are in parallel, the potential difference across each is the same, but the current is not. Then,
I = I1 + I2 + I3

Since charge is not accumulated at a point,

where Rp is the equivalent resistance of the combination. Therefore,

For the special case of only two resistors in parallel, the expression for the equivalent resistance takes on a particularly simple form, i.e.,


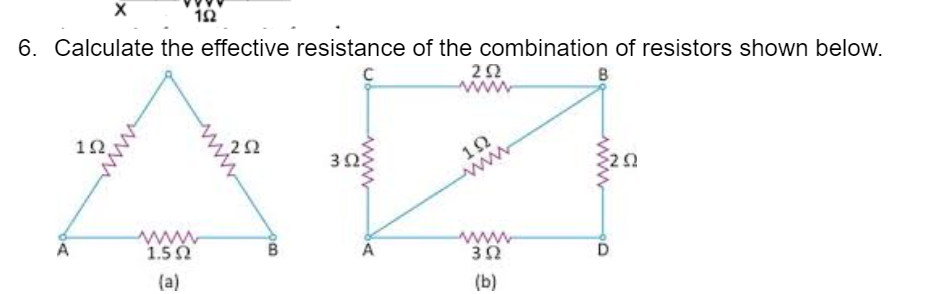
The first network can be simplified by replacing the parallel combination of R2 and R3 with its equivalent resistance. This is then in series with R1.
In the second network, the combination of R2 and R3 in series forms a simple parallel combination with R1.
But, not all networks can be reduced to simple series - parallel combinations, and special methods are required.